Calculo numérico - ponto flutuante

a

a) A representação será:

\(% MathType!MTEF!2!1!+- % feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbt9wDYn % wzGmvyUnhiqj3BaeXatLxBI9gBaerbd9wDYLwzYbItLDharuavP1wz % ZbItLDhis9wBH5garqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbb % L8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yqaqpe % pae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabeqaam % aaeaqbaaGceaabbeaaqaaaaaaaaaWdbiaabccacaWGMbGaamiBa8aa % daqadaqaa8qacaWG4bGaey4kaSIaamyEaaWdaiaawIcacaGLPaaape % Gaaeiiaiabg2da9iaadIhacqGHRaWkcaWG5bGaeyisISRaamiEaiab % gwPiflaabccacaWG5baabaGaamOzaiaadYgacaGGOaGaamOCaiaacM % cacqGH9aqpdaqadaqaamaalaaabaWaaOaaaeaacaaIXaGaey4kaSIa % amiEaaWcbeaakiabgkHiTiaaigdaaeaacaWG4baaaaGaayjkaiaawM % caamaalaaabaWaaOaaaeaacaaIXaGaey4kaSIaamiEaaWcbeaakiab % gUcaRiaaigdaaeaadaGcaaqaaiaaigdacqGHRaWkcaWG4baaleqaaO % Gaey4kaSIaaGymaaaaaeaacaWGMbGaamiBaiaacIcacaWGYbGaaiyk % aiabg2da9maalaaabaWaaeWaaeaadaGcaaqaaiaaigdacqGHRaWkca % WG4baaleqaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGa % eyOeI0IaaGymaaqaaiaadIhacaGGOaWaaOaaaeaacaaIXaGaey4kaS % IaamiEaaWcbeaakiabgUcaRiaaigdacaGGPaaaaaqaaiaadAgacaWG % SbGaaiikaiaadkhacaGGPaGaeyypa0ZaaSaaaeaacaaIXaaabaWaaO % aaaeaacaaIXaGaey4kaSIaamiEaaWcbeaakiabgUcaRiaaigdaaaaa % aaa!7FDA! \begin{array}{c} {\rm{ }}fl\left( {x + y} \right){\rm{ }} = x + y \approx x \oplus {\rm{ }}y\\ fl(r) = \left( {\frac{{\sqrt {1 + x} - 1}}{x}} \right)\frac{{\sqrt {1 + x} + 1}}{{\sqrt {1 + x} + 1}}\\ fl(r) = \frac{{{{\left( {\sqrt {1 + x} } \right)}^2} - 1}}{{x(\sqrt {1 + x} + 1)}}\\ fl(r) = \frac{1}{{\sqrt {1 + x} + 1}} \end{array}\)

b) 

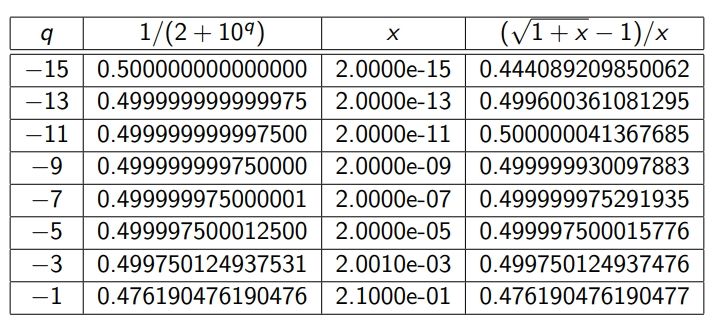
c)

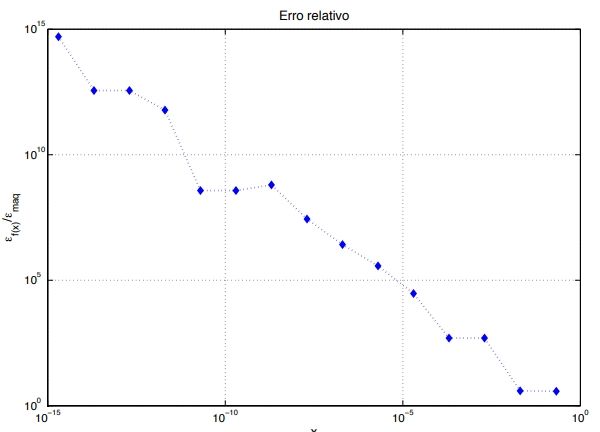
d)

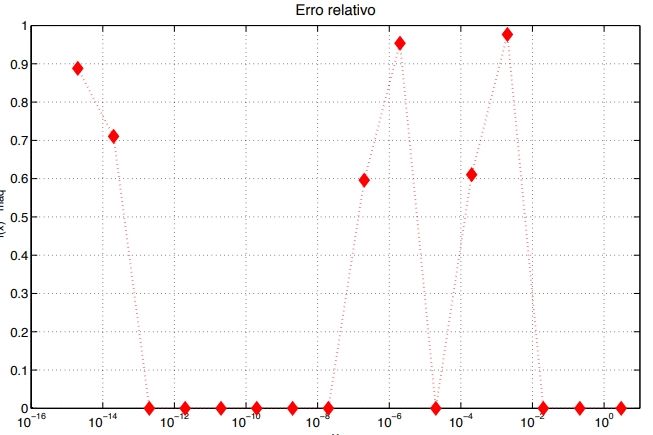
e) 

\(\begin{array}{l} {e_{maior}} = {2^{ - 23}} = 1,19 \cdot {10^{ - 7}}\\ {e_{menor}} = {2^{ - 52}} = 2,22 \cdot {10^{ - 16}} \end{array}\)