como calcular
Ache a equação da circunferencia que passa pelos pontos A,B e D nos seguintes casos A(6,2) B(4,0) e D (10,4)
💡 4 Respostas
Andre Smaira
Vamos encontrar a equação da circunferência que passa por três pontos  ,
,  e
e  , utilizando nosso conhecimento em equação reduzida da circunferência, dada abaixo, e sistema de equações.
, utilizando nosso conhecimento em equação reduzida da circunferência, dada abaixo, e sistema de equações.
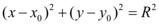
Para o ponto 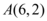 , aplicaremos
, aplicaremos  e
e  na equação reduzida da circunferência. Assim:
na equação reduzida da circunferência. Assim:
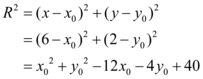
(I)
Agora, para o ponto 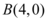 , aplicaremos
, aplicaremos  e
e na equação reduzida da circunferência. Assim:
na equação reduzida da circunferência. Assim:
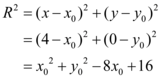
(II)
E, por último, para o ponto 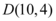 , aplicaremos
, aplicaremos  e
e na equação reduzida da circunferência. Assim:
na equação reduzida da circunferência. Assim:
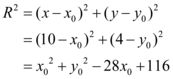
(III)
Para encontrar 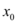 , podemos igualar as equações
, podemos igualar as equações  e
e  . Assim:
. Assim:
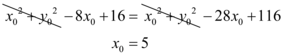
Para encontrar 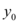 , podemos igualar as equações
, podemos igualar as equações  e
e  . Assim:
. Assim:
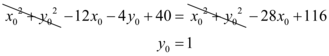
E, para encontrar  , vamos substituir os valores de
, vamos substituir os valores de 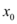 e
e 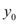 na equação
na equação  . Assim:
. Assim:
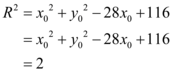
De onde 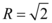 .
.
Por último, aplicando os valores de 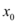 ,
, 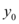 e
e  na equação reduzida da circunferência, temos:
na equação reduzida da circunferência, temos:
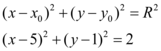
Portanto, a equação da circunferência que passa pelos pontos  ,
,  e
e  é representada por
é representada por 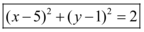 .
.
Gabriela Rodrigues
A equação de uma circunferência de centro (x0, y0) e raio R é
(x - x0)2 + (y - y0)2 = R2
Como A, B e D pertencem a circunferencia, temos:
(6 - x0)2 + (2 - y0)2 = R2 ==> 36 - 12x0 + x02 + 4 - 4y0 + y02 = R2 (1)
(4 - x0)2 + (0 - y0)2 = R2 ==> 16 - 8x0 + x02 + y02 = R2 (2)
(10 - x0)2 + (4 - y0)2 = R2 ==> 100 - 20x0 + x02 + 16 - 8y0 + y02 = R2 (3)
Pelas equações (1) e (2) temos
36 - 12x0 + x02 + 4 - 4y0 + y02 = 16 - 8x0 + x02 + y02 ==> 4x0 + 4y0 = 24 ==> 2x0 + 2y0 = 12 (4)
Pelas equações (2) e (3) temos
16 - 8x0 + x02 + y02 = 100 - 20x0 + x02 + 16 - 8y0 + y02 ==> 12x0 + 8y0 = 100 ==> 3x0 + 2y0 = 25 (5)
Subtraindo (4) de (5) encontramos x0 = 13 e, substituindo em (4), obtemos y0 = -7
Usaremos esses valores na equação (2) para determinar o raio R:
R2 = 16 - 8x0 + x02 + y02 = 16 - 8*13 + 132 + ( -7)2 = 130
Assim, a equação da circunferência é (x - 13)2 + (y - (-7))2 = 130, isto é,
(x - 13)2 + (y + 7)2 = 130
Andre Smaira
Vamos encontrar a equação da circunferência que passa por três pontos ,
e
, utilizando nosso conhecimento em equação reduzida da circunferência, dada abaixo, e sistema de equações.
Para o ponto , aplicaremos
e
na equação reduzida da circunferência. Assim:
(I)
Agora, para o ponto , aplicaremos
e
na equação reduzida da circunferência. Assim:
(II)
E, por último, para o ponto , aplicaremos
e
na equação reduzida da circunferência. Assim:
(III)
Para encontrar , podemos igualar as equações
e
. Assim:
Para encontrar , podemos igualar as equações
e
. Assim:
E, para encontrar , vamos substituir os valores de
e
na equação
. Assim:
De onde .
Por último, aplicando os valores de ,
e
na equação reduzida da circunferência, temos:
Portanto, a equação da circunferência que passa pelos pontos ,
e
é representada por
.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar