frações
1/4 dos funcionários de uma empresa dominam a informática. Dentre esses, a terça parte é mulher e os homens
são 10. Do total de funcionários dessa empresa 1/15 são funcionários administrativos. Nessa empresa, ocupam
esse cargo:
A) 4 funcionários.
B) 6 funcionários.
C) 5 funcionários.
D) 7 funcionários.
💡 5 Respostas
Leonardo Moreno
Opa!
Eu entendi o problema como “quantos funcionários administrativos há na empresa?”
Sendo assim, parti da seguinte forma:
No setor de informática há 10 homens e o restante é formado por mulheres, esse restante representa a terça parte, ou 1/3. Primeiro eu achei o total de funcionários neste setor. Você pode fazer com uma simples proporção:
10/x = 2/3.
Logo, 2*x = 10*3
x= 30/2 = 15
No setor de informática há 15 funcionários, sendo 10 homens e 5 mulheres.
Sabemos que esse 15 funcionários fazem parte de 1/4 da empresa. De forma semelhante a de cima podemos achar o número total de funcionarios da empresa. Vamos chamar de “t”.
15/t = 1/4
t= 15*4 = 60
Como 1/15 são funcionários administrativos (”a”):
a/60 = 1/15
15*a = 60*1
a= 60/15 = 4
Ao todo são 4 funcionários administrativos.
Qualquer outra duvida relacionada é só perguntar.
Um abração.
Leonardo.
Andre Smaira
Razão e Proporção
Razão
Duas grandezas podem ser comparadas. Dadas duas grandezas, a divisão entre essas grandezas é chamada de \(k\) , que é uma constante.
Exemplo:
- a razão entre 50 e 10: \(k = {{50} \over {10}} = 5\)
- a razão entre 4 e 20: \(k = {4 \over {20}} = {1 \over 5}\)
Proporção
Porporção é uma relação de igualdade entre duas razões.
Exemplos:
\[\eqalign{ & k = {4 \over 7} = {{28} \over {49}} \cr & k = {{11} \over {15}} = {{33} \over {45}} \cr}\]
Propriedade da Proporção
Seja dada uma igualdade entre duas razões, então temos que, se:
\[k = {A \over B} = {C \over D}\]
então:
\[A.D = B.C\]
Para resolver este exercício, primeiro temos que calcular o total de funcionários da empresa.
Seja \(x\) o número de funcionários da empresa, sabemos que \({1 \over 4}\) dos funcionários dominam a informática.
Desses \({1 \over 4}\) dos funcionários, \({1 \over 3}\) são mulheres, logo temos que:
\[1 - {1 \over 3} = {3 \over 3} - {1 \over {12}} = {2 \over 3}\]
Ou seja, \({2 \over {3}}\) dos funcionários que dominam a informática são homens. Esses \({2 \over {3}}\) correspondem a 10 homens.
Portanto, temos que:
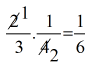
1561857900256
Ou seja, \({1 \over 6}\) corresponde ao número de homens que dominam a informática. Portanto:
\[\eqalign{ & {1 \over 6}x = 10 \cr & x = 10.6 \cr & x = 60 \cr}\]
Logo, na empresa há 60 funcionários.
Agora temos que calcular o números de funcionários administrativos existem, sabendo que esses correspondem a \({1 \over {15}}\) da empresa. Vamos chamar de \(y\) esses funcionários.
\[\eqalign{ & y = {1 \over {15}}.60 \cr & y = 4 \cr}\]
Portanto temos que o número de funcionários que trabalham da parte administrativa desta empresa é de:
A) 4 funcionários.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.






Compartilhar