me ajudem com essas equações de Cauchy-Euler !! Obrigada

Question

x&sup2;y''-3xy'+4y=x&sup2;lnxx&sup2;y''-5xy'+9y=0

Aristóteles Junio · Answer

x^2y"-5xy'+9y=0
primeiro vc deriva y(t)=t^m = y'(t)=mt^m-1.  faz a segunda derivada
y"(t)=m(m-1)t^m-2.
substitui na equação anterior irá ficar.
t^2(m(m-1)t^m-2)-5t(mt^m-1)+9t^m=0
organizando .
m(m-1)t^m-5mt^m+9t^m=0
colocando t^m em evidência.
t^m(m(m-1)-5m+9)=0 . analisamos que t^m tem que ser igual a zero e se ele multiplica todo o momento em parentese o número em parentese é igual a zero , então fica,
m(m-1)-5m+9=0
fazendo as operações irá da uma equação de segundo grau.
m^2-6m+9=0 fazendo baskara achamos uma raiz só x=3 então a solução será y(x)=c1t^3+c2t^3ln(x). espero ter ajudado, qualquer dúvida pergunta a outra questão estou com preguiça de fazer kkkkk

yuri miguel · Answer

Fazendo y=ux^3, y'=3ux^2+u'x^3,
y"=6u'x^2+u"x^3+6ux

Subistituindo na equacao dada 
X^2y"- 5xy'+ 9y=0
X^2(6u'x^2+u"x^3+6ux)-5x(3ux^2+u'x^3)+9ux^3=0
u"x^5+u'x^4=0, onde w=u', w'=u"
W'x^5+wx^4=0-> dw/w=-dx/x
W=c/x -> w=u', c/x=du/dx
u=c*ln(x)+k , se y=ux^3 entao y=cx^3ln(x)+kx^3

RD Resoluções · Answer

Sabemos que, para resolver a Equação de Cauchy-Euler

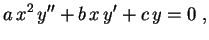
devemos começar procurando uma solução da forma 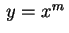. Substituindo em (1) vemos que  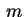deve ser raiz da equação algébrica

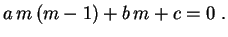
Suponhamos que a equação acima tenha raízes complexas 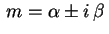. Com elas construímos duas soluções linearmente independentes da primeira equação,

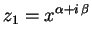e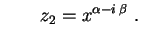

Já tínhamos trabalhado com exponenciais com expoente complexo, mas de base 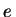. É fácil dar um sentido às exponenciais acima, cuja base não é :

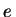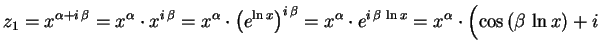
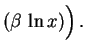
Analogamente obtemos

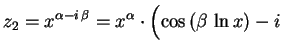sen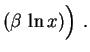

As duas soluções 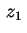 e 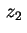 da primeira equação encontradas acima são linearmente independentes mas assumem valores complexos, o que pode ser um inconveniente para algumas aplicações. Por esta razão, vamos preferir as combinações lineares delas

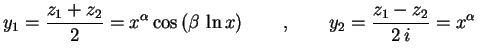
que são linearmente independentes e reais.

me ajudem com essas equações de Cauchy-Euler !! Obrigada

Cálculo III

ESTÁCIO

💡 2 Respostas

Faça como milhares de estudantes: teste grátis o Passei Direto

Agora você pode testar o

Passei Direto grátis

✏️ Responder

Outros materiais

Perguntas relacionadas

Equações de Cauchy-Euler são aquelas que podem ser escritas na forma:?

Para encontrar a solução das Equações de Cauchy-Euler homogêneas de segunda ordem, precisamos resolver a equação característica:?

1 – AVALIAÇÃO I – CÁLCULO DIFERENCIAL IV Para encontrar a solução das Equações de Cauchy-Euler homogêneas de segunda ordem, precisamos resolver a e...

Para encontrar a solução das Equações de Cauchy-Euler homogêneas de segunda ordem, precisamos resolver a equação característica: A Somente a senten...

Materiais relacionados

Outros materiais