Como para derivar as equacoes de tensao e corrente atraves de um circuito LC?

Isso não tem nada a ver com a energia armazenada por L e C como Rick sugere. Para encontrar a corrente que você precisa saber a tensão da fonte e substituindo a impedância Z R v = IR localizar o atual. Uma vez que a corrente é conhecida também sabemos que mesmo atual existe tudo ao longo da cadeia de série e para encontrar a tensão através de uma das reatâncias temos que multiplicar a corrente pelo valor ohmico sendo examinado. A energia transferida do L c pode ser qualquer quantidade e não tem nada a ver com esse problema. A transferência de energia entre L e C pode ser ainda maior, em seguida, as despesas reais de energia como calor como eu ^ perda de 2R, tudo isso depende a qualidade Q do circuito.

A figura abaixo mostra um circuito do tipo LC. No circuito (a), colocamos a fonte em contato apenas com o capacitor para carregá-lo. Após o carregamento completo do capacitor, desligamos a chave do ponto A e ligamos no ponto B desconectando a fonte do circuito. Mesmo assim o capacitor permanece carregado.

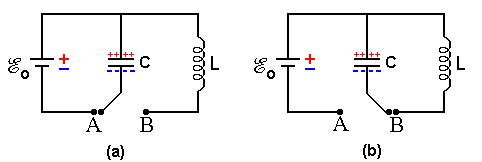
A ligação da chave no ponto B faz com que apareça uma corrente no circuito. Esta corrente passará pelo indutor criando consequentemente campos magnéticos. Isto significa que, parte da energia que estava armazenada no capacitor é transformada em energia magnética no indutor. 
 

A seguir, mostraremos que é possível encontrar uma equação que descreva o comportamento temporal das cargas e correntes no novo circuito.  Existem vários métodos para resolver este problema. Um deles seria usar as leis de Kirchhoff como no caso anterior. Neste caso, diferentemente, determinaremos as equações para q e i usando a lei de conservação de energia, como a seguir.

Sabemos que as energias armazenadas num capacitor e num indutor são respectivamente dadas por;

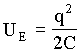                    e                                                       (1)

Como o sistema é fechado e ideal, temos que a energia total (U_T) no circuito é uma constante. Como existem apenas dois elementos no circuito, podemos afirmar que a energia total, deve ser uma soma das energias elétrica (U_E) e magnética (U_B), produzidas no capacitor e no indutor respectivamente. Assim temos que;

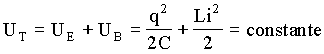                                                            (2)

Derivando ambos lados da equação acima em função do tempo temos que;

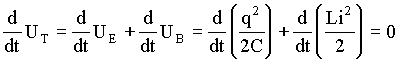                                                  (3)

ou de uma forma mais simplifica;

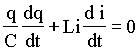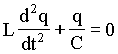             ou                                                  (4)

A equação acima é uma equação diferencial de segunda ordem, incompleta e homogênea. Como no caso anterior, existem vários métodos de resolve-la. Analisando a equação diferencial acima notamos que a derivada segunda de q(t) é a própria função q(t), a menos de algumas constantes. Isto sugere, intuitivamente, que a que a solução desta equação diferencial deve ser uma função do tipo seno, cosseno ou combinações delas. Com base nisto assumimos que q(t) em função do tempo seja da forma;

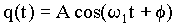                                                                         (5)

onde A , w₁ e f são constantes a serem determinadas, usando condições adicionais.  Inicialmente, como condição de contorno, assumimos que para o instante t = 0 a carga no capacitor é máxima, isto é q(t=0) = q_o =A e a fase f = 0. 
    Substituindo esta equação para q(t) na equação diferencial acima, podemos facilmente verificar que q(t) é uma solução para (16). Isto é;

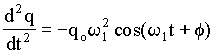                                                                   (6)

e

   .                                                (7)

Isto implica a constante w₁ pode ser determinada. Neste caso podemos dividir ambos lados da equação por 
Lq_ocos(w₁t+f ) o implica em;

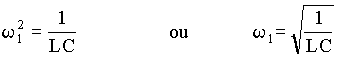       .                                                  (8)

Observamos com isto que w₁ deve ser a freqüência angular de oscilação do circuito. A freqüência angular depende apenas da indutância e capacitância do circuito LC. Como a carga do circuito é variável no tempo consequentemente a corrente será também dependente do tempo.

Para verificar esta afirmação, basta derivar a equação (17) em função de t. Isto é;

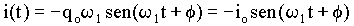                                                         (9)