Como como fazer regra de cramer

A regra de Cramer é um teorema em álgebra linear, que dá a solução de um sistema de equações lineares em termos de determinantes. Recebe este nome em homenagem a Gabriel Cramer (1704 - 1752).

Se {\displaystyle A{\vec {x}}={\vec {b}}} é um sistema de {\displaystyle n} equações e {\displaystyle n} incógnitas. (Onde {\displaystyle A} é a matriz de coeficientes do sistema, {\displaystyle {\vec {x}}} é o vetor coluna das incógnitas e {\displaystyle {\vec {b}}} é o vetor coluna dos termos independentes)

Então {\displaystyle \forall j,1\leq j\leq n}, a solução do sistema {\displaystyle x_{j}} é dada por:

{\displaystyle x_{j}={\left|A_{j}\right| \over \left|A\right|}={det(A_{j}) \over det(A)}}

Em que Aj é a matriz que se obtém da matriz A substituindo a coluna j pela coluna dos termos independentes b.

Dado um sistema de equações lineares, a Regra de Cramer é uma maneira prática de resolver apenas uma das variáveis sem ter que resolver todo o sistema de equações. Eles não costumam ensinar a Regra de Cramer dessa maneira, mas este é o ponto da Regra: em vez de resolver todo o sistema de equações, você pode usar o Cramer para resolver apenas uma única variável.

Vamos usar o seguinte sistema de equações:

     2x + y + z = 3
       x - y - z = 0
       x + 2y + z = 0

Temos o lado esquerdo do sistema com as variáveis (a "matriz de coeficiente") e o lado direito com os valores de resposta. Seja D o determinante da matriz de coeficientes do sistema acima, e seja Dx o determinante formado pela substituição dos valores de x-column pelos valores da coluna de resposta:

Temos o lado esquerdo do sistema com as variáveis (a "matriz de coeficiente") e o lado direito com os valores de resposta. Seja D o determinante da matriz de coeficientes do sistema acima, e seja Dx o determinante formado pela substituição dos valores de x-column pelos valores da coluna de resposta:

sistema de
equações
2x + 1y + 1z = 3
 1x – 1y – 1z = 0
1x + 2y + 1z = 0

coeficiente
matriz de
determinante

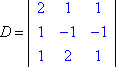
coluna resposta
[[3]

[0]

[0]]

Dx: coeficiente determinante
com coluna de resposta
valores na coluna x

[[3]   1      1

[0]     -1    -1

[0]]     2       1

Da mesma forma, Dy e Dz seriam então: Copyright © Elizabeth Stapel 2004-2011 Todos os direitos reservados.

     D_y =

2  3 1

1 0 -1

1 0 1

     D_z =

2  1 3

1 -1  0

1 1  0

Avaliando cada determinante, obtemos:

     D = 3

     D_x = 3

     D_y = -6

     D_z = 9

A Regra de Cramer diz que x = Dx ÷ D, y = D ÷ D e z = Dz ÷ D. Ou seja:

     x = 3/3 = 1, y = –6/3 = –2 ez = 9/3 = 3

exemplo:

Dado o seguinte sistema de equações, encontre o valor de z.

2x + y + z = 1
x - y + 4z = 0
x + 2y - 2z = 3

Para resolver apenas para z, primeiro encontro o coeficiente determinante utilizand as tres colunas principais do lado esquerdo da equação.

D = -3

Em seguida, forme Dz substituindo a terceira coluna de valores pela coluna a direita da equação.

D_z = -6


Então eu formulo o quociente e simplifico:





Dz / D = -6 / -3 = 2

z = 2