AJUDA PARA RESOLVER TRABALHO
Para uma viga calcular para o momento fletor máximo a área de armadura longitudinal de flexão e as deformações na fibra de concreto mais comprimidas e na armadura de flexão tracionada. Sao conhecidos:
Mk máx = 10.000kN.m
h = 50cm
Yc=Yf = 1,4
Ys=1,15
bw=20cm
concreto C20 (fck = 20MPa)
d = 47 cm (altura útil)
aço CA-50
c = 2,0 cm (cobrimento nominal)
φt= 5mm (diametro estribo)
d máx=19mm
💡 3 Respostas
RD Resoluções
O enunciado não especifica os apoios da viga, vamos considerar o seguinte:
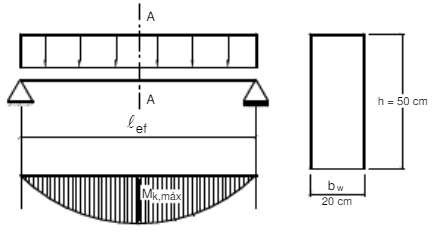
Figura 1 - Representação da viga, em uma situação biapoiada.
Vamos considerar, ainda, que o momento fletor caracterísico máximo seja 10.000kN.cm, e não 10.000kN.m.
A questão é bastante extensa, e será feita passo a passo, com explicações, a fim de garantir o entendimento e não apenas "jogar" as contas. Devemos considerar os seguintes conceitos:
- O momento fletor de cálculo pode ser calculado por $M_d = \gamma_f * M_k$, onde:
- $M_d$ é o momento fletor de cálculo;
- $\gamma_f$ é o coeficiente de segurança que majora os esforços solicitantes; e
- $M_k$ é o momento fletor característico.
-
O valor que delimita os domínios 2 e 3 é dado por $x_{2lim}$, definido na Eq. 30 da apostila de “Fundamentos do Concreto Armado” (BASTOS, 2011), sendo $x_{2lim}$ fixo e igual a $0,26*d$, sendo $d$ a altura útil;
-
A delimitação entre os domínios 3 e 4 é dada por $x_{3lim}$. Para o aço CA-50, conforme a Tabela 1, $x_{3lim}$ é $x_{3lim} = 0,63*d$, sendo $d$ a altura útil;
-
O momento interno resistente proporcionado pelo concreto comprimido pode ser calculado por $M_d = 0,68 * b_w *f_{cd} * (d - 0,4*x)$, onde:
-
$M_d$ é o momento, em valor absoluto;
-
$b_w$ é a largura da seção;
-
$x$ é a posição da linha neutra;
-
$f_{cd}$ é a resistência de cálculo do concreto à compressão; e
-
$d$ é a altura útil.
-
-
As deformações nos materiais componentes das vigas de concreto armado submetidas à flexão simples encontram-se nos domínios de deformações 2, 3 ou 4, conforme definidos na NBR 6118/03. Tem-se as figuras:
-
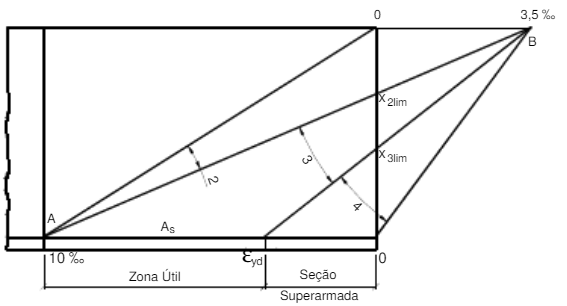 Figura 2 - Diagrama de deformações dos domínios 2, 3 e 4.
Figura 2 - Diagrama de deformações dos domínios 2, 3 e 4. -
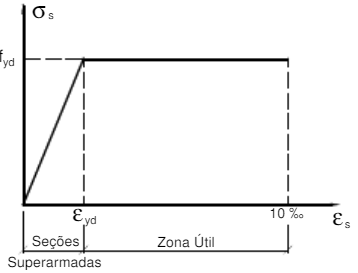 Figura 3 - Zonas de dimensionamento em função da deformação no aço.
Figura 3 - Zonas de dimensionamento em função da deformação no aço.
-
-
A área da armadura tracionada pode ser calculada por $A = \dfrac{M_d}{\sigma_{sd}*(d-0,4*x)}$, onde:
-
$A$ é a área da armadura;
-
$\sigma_{sd}$ é a tensão na armadura tracionada;
-
$d$ é a altura útil; e
-
$x$ é a posição da linha neutra.
-
-
Nas equações do tipo K devem ser obrigatoriamente consideradas as unidades de kN e cm para as variáveis. $K_C$ pode ser calculado por $K_C = \dfrac{b_w * d^2}{M_d}$, onde $b_w$ é a largura da seção, e as outras variáveis são as mesmas adotadas anteriormente.
-
Considerando-se a variável $β_x$, que relaciona a posição da linha neutra com a altura útil $d$, tem-se $\beta_x = \dfrac{x}{d}$.
-
A área de armadura tracionada $A_s$, em função do coeficiente $K_s$, é $A_s = K_s * \dfrac{M_d}{d}$.
-
Do diagrama de deformações, define-se a relação entre as deformações de cálculo na armadura ($ε_{sd}$) e no concreto correspondente à fibra mais comprimida:
-
$\dfrac{\epsilon_{cd}}{\epsilon_{sd}} = \dfrac{x}{d - x}$.
-
-
Considerar como Tabela 1 de Valores de $K_c$ e $K_s$ para o aço CA-50, disponível em http://www.fec.unicamp.br/~almeida/ec702/Tabelas/tab%201%20-%20kc%20e%20ks.pdf, acesso 24 de Julho de 2018.
-
Considerar como Tabela 2 a tabela Taxas mínimas de armadura de flexão para vigas, da NBR 6118;
-
Considerar como Tabela 3 a tabela Características de fios e barras, da NBR 7480/96.
-
Considerar como Tabela 4 a tabela Área de aço e largura $b_w$ mínima, disponível em http://www.set.eesc.usp.br/mdidatico/concreto/Textos/20%20Tabelas%20gerais.pdf. Acesso em 24 de Julho de 2018.
-
Os conceitos e explicações usadas são baseadas na apostila Notas de Aula de Flexão Normal Simples - Vigas, da Disciplina Estruturas de Concreto I, do Prof. Dr. Paulo Sérgio dos Santos Bastos.
O momento fletor de cálculo será
$M_d = \gamma_f * M_k = 1,4 * 10.000kN.cm = 14.000 kN.cm$;
O valor que delimita os domínios 2 e 3 será $x_{2lim} = 0,26* d = 0,26 * 47 cm = 12,2cm$;
A delimitação entre os domínios 3 e 4 será $x_{3lim} = 0,63 * d = 0,63 * 47cm \approx 29,6cm$;
Vamos agora determinar a posição $x$ da linha neutra para a seção:
$M_d = 0,68 * b_w *f_{cd} * (d - 0,4*x) \Rightarrow 14.000 = 0,68 * 20 * \dfrac{20}{1,4}*(47 - 0,4*x)$
$x^2 - 117,5*x + 1.801,8 = 0 \Rightarrow \begin{cases}x_1 = 99,4cm\\ x_2 = 18,1cm \end{cases}$.
A primeira raiz não nos será últil, já que seu valor é maior que a altura da seção. Assim, $x = 18,1cm$, e, como o momento fletor solicitante tem sinal positivo, a posição da linha neutra deve ser medida a partir da borda superior comprimida.
É importante observar que o momento fletor deve ser colocado na equação com o seu valor absoluto. O momento fletor positivo traciona a parte inferior da viga, e para resistir a ele é colocada uma armadura longitudinal chamada “armadura positiva”. No caso de momento fletor negativo é colocada a “armadura negativa”, próxima à borda superior da viga.
Comparando a posição da linh a neutra $x$ com os limites $x _{2lim}$ e $x_{3lim}$, determina-se o domínio em que a viga se encontra:
$x _{2lim} = 12,2cm < x = 18,1cm < x_{3lim} = 29,6cm$.
Como a seção não é de apoio ou de ligação com outro elemento estrutural, o limite $x/d \leq 0,5$ (para concretos até o C35 como neste exemplo) não necessita ser atendido.
Como a linha neutra está no intervalo entre $x _{2lim}$ e $x_{3lim}$, verifica-se que a viga está no domínio 3, domínio no qual deformação na armadura varia de $\epsilon_{yd}$ (início de escoamento do aço) a $10$ ‰ (conforme Figura 2).
Conforme o diagrama σ por ε do aço (Figura 3), a tensão nesta faixa de deformação é $σ_{sd}= f_{yd} = f_{yk}/γ_s$ (para o aço CA-50, $f_{yk} = 50 kN/cm^2 = 500 MPa$). Calculamos a área da armadura:
$A = \dfrac{M_d}{\sigma_{sd}*(d-0,4*x)} = \dfrac{14.000}{\frac{50}{1,15}*(47 - 0,4*18,10)} \Rightarrow A = 8,10cm^2$.
Teremos a seguinte situação:
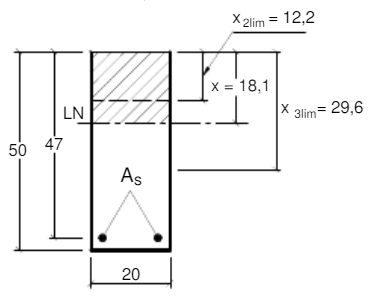
Figura 4 - Posição da linha neutra na seção transversal e limites entre os domínios 2, 3 e 4.
Apenas a título de comparação, vamos calcular a área da armadura por meio de equações com coeficientes K.
Teremos $K_c = \dfrac{b_w * d^2}{M_d} = \dfrac{20 * 47^2}{14.000} = 3,2$.
Com $K_c = 3,2$, concreto C20 e aço C A-50, na Tabela 1 determinam-se os coeficientes $β_x = 0, 38$, $K_s = 0,027$ e domínio 3.
Determina-se a posição da linha neutra por
$\beta_x = \dfrac{x}{d} \Rightarrow x = \beta_x * d = 0,38 * 47 = 17,9cm$.
A área da armadura, por sua vez, será
$A_s = K_s * \dfrac{M_d}{d} = 0,027 * \dfrac{14.000}{47} = 8,04cm$.
Vemos que o valor é bastante próximo ao calculado pelas equações teóricas.
Agora, vamos verificar o detalhamento da armadura na seção transversal.
Vamos comparar a armadura calculada ($A_s = 8,10 cm^2$) com a armadura mínima longitudinal prescrita pela NBR 6118/ 03. De acordo com a Tabela 2, para concreto C20 e seção retangular, pode-se considerar a armadura mínima de flexão como:
$A_{s,mín} = 0,15 % * b_w * h = 0,0015 * 20 * 50 = 1,5cm^2$.
Assim, a armadura calculada é maior que a mínima. Se a mínima fosse maior, usaríamos seu valor. A escolha do diâmetro ou dos diâmetros e do número de barras para atender à área de armadura calculada admite diversas possibilidades. Um ou mais diâmetros podem ser escolhidos, preferencialmente valores próximos entre si. A área de aço escolhida deve atender à área de armadura calculada, preferencialmente com uma pequena folga, mas segundo sugestão do Prof. Dr. Paulo Sérgio dos Santos Bastos, admite-se uma área até 5 % inferior à calculada.
O número de barras deve ser um que não resulte numa fissuração significativa na viga e nem dificuldades adicionais durante a confecção da armadura. A fissuração diminui quanto mais barras finas são utilizadas, porém, não devem ocorrer exageros.
Para a área de armadura calculada no exercício, de $8,10 cm^2$, com auxílio das Tabelas 3 e 4, podem ser enumeradas as seguintes combinações:
- $16 φ 8 mm = 8,00 cm^2$;
- $10 φ 10 mm = 8,00 cm^2;7 φ 12,5 mm = 8,75 cm^2$;
- $4 φ 16 mm = 8,00 cm^2$;
- $3 φ 16 mm + 2 φ 12,5 mm = 8,50 cm^2$;
- $3 φ 20 mm = 9,4 5 cm^2$;
- $2 φ 20 mm + 1 φ 16 mm = 8,30 cm^2$;
- $2 φ 20 mm + 2 φ 12,5 mm = 8,80 cm^2$.
Outras combinações de número de barras e de diâmetros podem ser enumeradas, e a escolha de uma delas deve levar em conta os fatores fissuração, facilidade de execução, porte da obra, número de camadas de barras, exequibilidade (largura da viga principalmente), entre outros.
Detalhamentos com uma única camada resultam seções mais resistentes que seções com duas ou mais camadas de barras, pois quanto mais próximo estiver o centro de gravidade da armadura à borda tracionada, maior será a resistência da seção. Define-se como camada as barras que estão numa mesma linha paralela à linha de borda da seção. O menor número possível de camadas deve ser um dos objetivos do detalhamento.
Das combinações listadas, 16 φ 8 e 10 φ 10 devem ser descartadas porque o número de barras é excessivo, o que aumentaria o trabalho do armador (op erário responsável pela confecção das armaduras nas construções). Por outro lado, as três últimas combinações, com o diâmetro de 20 mm, têm um número pequeno de barras, não sendo o ideal para a fissuração, além do fato da barra de 20 mm representar maiores dificuldades no seu manuseio, confecção de ganchos, etc.
Entre todas as combinações, as melhores alternativas são 7 φ 12 ,5 e 4 φ 16 mm, sendo esta última pior para a fissuração, mas que certamente ficará dentro de valores máximos recomendados pela NBR 6118/03.
Na escolha entre 7 φ 12,5 e 4 φ 16 mm deve-se também atentar para o porte da obra. Construções de pequeno porte devem ter especificados diâmetros preferencialmente até 12,5 mm, pois a maioria delas não têm máquinas elétricas de corte de barras, onde são cortadas com serras ou guilhotinas manuais, com capacidade de corte de barras até 12,5 mm. Guilhotinas maiores são praticamente inexistentes nas obras de pequeno porte. Além disso, as armaduras são feitas por pedreiros e ajudantes e não armadores profissionais. Não há também bancadas de trabalho adequadas para o dobramento das barras, de modo que são recomendados diâmetros de até 12,5 mm para as obras de pequeno porte, e acima de 12,5 mm apenas para as obras de maior porte, com trabalho de armadores profissionais.
Como o momento fletor solicitante tem sinal positivo, é extremamente importante que a armadura $A_s$ calculada seja disposta na posição correta da viga, isto é, nas proximidades da borda sob tensões de tração, que no caso em questão é a borda inferior. Um erro de posicionamento da armadura, como as barras serem colocadas na borda superior, pode resultar no sério comprometimento da viga em serviço, podendo-a levar inclusive ao colapso imediatamente após a retirada dos escoramentos.
A disposição das barras entre os ramos verticais do estribo deve proporcionar uma distância livre entre as barras suficiente para a passagem do concreto, a fim de evitar o surgimento de nichos de concretagem, chamados na prática d e “bicheira”. Para isso, o espaçamento livre horizontal mínimo entre as barras é dado por $e_{h,min} \geq \begin{cases}2cm\\ \phi_l\\ 1,2*d_{max,agr} \end{cases}$.
Quando as barras de uma mesma camada têm diâmetros diferentes, a verificação do espaçamento livre mínimo ($e_{h,min}$) entre as barras deve ser feita aplicando-se a equação acima. Por outro lado, quando as barras da camada têm o mesmo diâmetro, a verificação pode ser feita com auxílio da Tabela 4, que mostra a “Largura $b_w$ mínima” para um dado cobrimento nominal ($c$). Determina-se a largura mínima na intersecção entre a coluna e a linha da tabela, correspondente ao número de barras da camada e o diâmetro das barras, respectivamente. O valor para a largura de $b_w$ mínimo depende do diâmetro máximo da brita de maior dimensão utilizada no concreto.
A Figura 5 mostra o detalhamento da armadura na seção transversal da viga, onde foi adotada a combinação 4 φ 16 mm.
Para 4 φ 1 6 mm, na Tabela 4 encontra-se a largura mínima de 19 cm para concreto com brita 1 e cobrimento de 2,0 cm. Como a largura da viga é 20 cm, maior que a largura mínima, é possível alojar as quatro barras numa única camada, atendendo ao espaçamento livre mínimo.
Além da armadura tracionada A$_s$ devem ser dispostas também no mínimo duas barras na borda superior da seção, barras construtivas chamadas “porta-estribos”, que servem para a amarração dos estribos da viga. Armaduras construtivas são muito comuns nos elementos estruturais de concreto armado, auxiliam na confecção e montagem das armaduras e colaboram com a resistência da peça, embora não sejam levadas em conta nos cálculos.
A distância $a$, medida entre o centro de gravidade da armadura tracionada e a fibra mais tracionada da seção transversal, neste caso é dada pela soma do cobrimento, do diâmetro do estribo e metade do diâmetro da armadura:
$a = 2,0 + 0,5 + \frac{1,6}{2} = 3,3cm$.
A altura útil $d$, definida como a distância entre o centro de gravidade da armadura tracionada à fibra mais comprimida da seção transversal, conforme o detalhamento da Figura 5, é:
$d = h - a = 50 - 3,3 = 46,7cm$.
O valor inicialmente adotado para a altura útil $d$ foi 47 cm. Existe, portanto, uma pequena diferença de 0,3 cm entre o valor inicialmente adotado e o valor real calculado em função do detalhamento escolhido. Pequenas diferenças, de até 1cm ou 2 cm podem, de modo geral, serem desconsideradas em vigas de dim ensões correntes, não havendo a necessidade de se recalcular a armadura, pois a diferença de armadura geralmente é pequena.
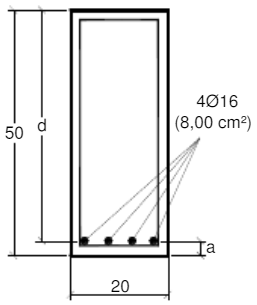 Figura 5. Detalhamento da armadura longitudinal $A_s$ na seção transversal.
Figura 5. Detalhamento da armadura longitudinal $A_s$ na seção transversal.
Por fim, vamos calcular as deformações na fibra de concreto mais comprimida e na armadura tracionada.
No domínio 3 a deformação de encurtamento na fibra $d$ e concreto mais comprimida é fixa e igual a 3,5 ‰.
A deformação na armadura $A_s$ varia de $\epsilon_{yd} (2,07 ‰ para o aço CA-50) a 10 ‰, podendo ser calculada pela equação abaixo. Considerando d = h – a = 50 – 3,3 = 46,7 cm:
$\dfrac{\epsilon_{cd}}{\epsilon_{sd}} = \dfrac{x}{d - x} \Rightarrow \dfrac{3,5}{\epsilon_{sd}} = \dfrac{18,1}{46,7 - 18,1} \Rightarrow \epsilon_{sd} = 5,5\%$.
A Figura 6 ilustra as deformações nos materiais e os domínios 2 e 3 de deformação.
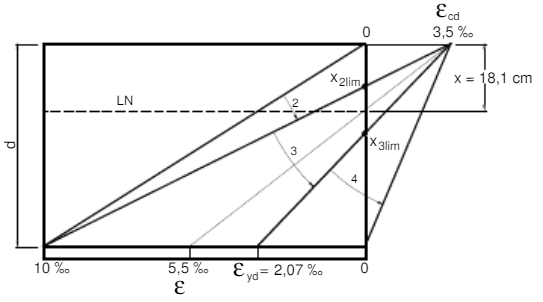
Figura 6 - Diagrama de domínios e deformações no concreto comprimido e na armadura tracionada.
Portanto, respondemos às três solicitações do enunciado:
- A área de armadura longitudinal de flexão é $\boxed{8,10cm^2}$;
- A deformação na fibras de concreto mais comprimidas é $\boxed{3,5‰}$; e
- A deformação na armadura de flexão tracionada é $\boxed{5,5‰}$.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Materiais relacionados
 340 pág.
340 pág. 6 pág.
6 pág.




Compartilhar