RESISTENCIA DOS MATERIAIS

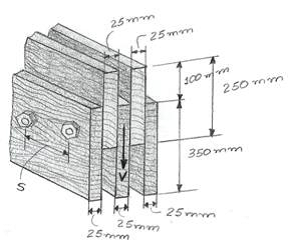
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.

	F = 5,31 KN
	F = 4,51 KN
	F = 3,31 KN
	F = 8,31 KN
	F = 3,51 KN

Resistência dos Materiais I

•

UNIUBE

0

1

Kessianny Gomes

29.03.2018

💡 1 Resposta

G7XS

10.04.2018

https://drive.google.com/open?id=1edtey6IPBYkVO--kg5eIqBRac_3Ek7x0

0

RD Resoluções

24.04.2018

Para encontrarmos a força de cisalhamento máxima, realizaremos os cálculos abaixo:

\(\begin{align} & \overset{-}{\mathop{y}}\,=\frac{\sum\limits_{{}}^{{}}{\overset{-}{\mathop{y}}\,A}}{\sum\limits_{{}}^{{}}{A}}=\frac{3(175(350\cdot 25))+2(325(250\cdot 25))}{3(350\cdot 25)+2(250\cdot 25)} \\ & \overset{-}{\mathop{y}}\,=223,3mm \\ & \\ & I=5,23\cdot {{10}^{-4}}{{m}^{4}} \\ & \\ & Q=\sum{\overset{-}{\mathop{y}}\,A}=2\left[ \left( 0,325-0,22 \right)(0,25\cdot 0,025 \right] \\ & Q=0,00127{{m}^{3}} \\ & \\ & q=\frac{VQ}{I} \\ & q=\frac{35\cdot 0,00127}{5,23\cdot {{10}^{-4}}} \\ & q=84,99KN/m \\ & \\ & \frac{q}{n}=\frac{F}{s} \\ & \frac{84,99}{4}=\frac{F}{0,25} \\ & F=5,31KN \\ \end{align}\ \)

0