fisica 3

Esboce um diagrama de corpo livre sobre  a carga que esta na origem. A carga de +19 µC causa uma força elétrica de atração sobre a carga que está na origem, força orientada no sentido negativo de x;

A carga de -57 µC exerce uma força de repulsão sobre a partícula que está na origem, força orientada no sentido negativo de x;

Logo a força total sobre a partícula será a soma dessas duas forças com um sinal negativo, pois ambas apontam no sentido negativo do eixo, vezes o vetor unitário î. Então basta usar a formula da lei de coloumb, transformando as distâncias em metros e vc terá a direção, sentido e módulo da força (vetor).

O módulo da força será o módulo do vetor obtido anteriormente.

Na figura abaixo representamos o sistema proposto no problema.

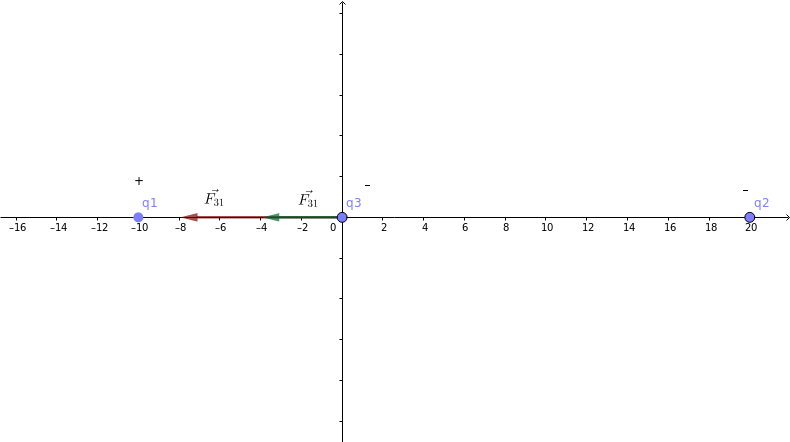
Na terceira partícula q₃ há duas forças elétricas atuando: a força de atração \(\vec F_{31}\) devido à carga q₁ e a força de repulsão \(\vec F_{32}\) devido à particula q₂.

A força resultante \(\vec F_{R3}\) na carga q₃ é dada por:

\(\vec F_{R3}=\vec F_{31}+\vec F_{32}\)   (1)

Calculando a força \(\vec F_{31}\), temos:

\(|\vec F_{31}|=\kappa{|q_1||q_3|\over d^2} = 9\times10^9\times{19\times 10^{-6}\times 3,8\times 10^{-6} \over 10^2} \approx6,50mN\)

onde k=9x10⁹ Nm²/C² é a constante eletrostática

Agora calculando a força \(\vec F_{32}\), temos:

\(|\vec F_{32}|=\kappa{|q_2||q_3|\over d^2} = 9\times10^9\times{57\times 10^{-6}\times 3,8\times 10^{-6} \over 20^2} \approx4,87mN\)

Portanto, como os vetores força são paralelos e têm o mesmo sentido, o módulo da força elétrica resultante na carga q₃ será dada por:

\(|\vec F_{R3}|=|\vec F_{31}|+|\vec F_{32}|=6,50\times 10^{-3}+4,87\times 10^{-3}=11,37mN\)

Na figura abaixo representamos o sistema proposto no problema.

Na terceira partícula q₃ há duas forças elétricas atuando: a força de atração \(\vec F_{31}\) devido à carga q₁ e a força de repulsão \(\vec F_{32}\) devido à particula q₂.

A força resultante \(\vec F_{R3}\) na carga q₃ é dada por:

\(\vec F_{R3}=\vec F_{31}+\vec F_{32}\)   (1)

Calculando a força \(\vec F_{31}\), temos:

\(|\vec F_{31}|=\kappa{|q_1||q_3|\over d^2} = 9\times10^9\times{19\times 10^{-6}\times 3,8\times 10^{-6} \over 10^2} \approx6,50mN\)

onde k=9x10⁹ Nm²/C² é a constante eletrostática

Agora calculando a força \(\vec F_{32}\), temos:

\(|\vec F_{32}|=\kappa{|q_2||q_3|\over d^2} = 9\times10^9\times{57\times 10^{-6}\times 3,8\times 10^{-6} \over 20^2} \approx4,87mN\)

Portanto, como os vetores força são paralelos e têm o mesmo sentido, o módulo da força elétrica resultante na carga q₃ será dada por:

\(|\vec F_{R3}|=|\vec F_{31}|+|\vec F_{32}|=6,50\times 10^{-3}+4,87\times 10^{-3} \\ |\vec F_{R3}|=11,37mN\)