Como calcular tranformada de Fourier?
💡 1 Resposta
RD Resoluções
A transformada de Fourier de uma função f(x) é definida como:
![${\cal{F}}[f(x)] \equiv F(w_x) = \int_{-\infty}^\infty
f(x) e^{-2i\pi w_xx} dx$](http://astro.if.ufrgs.br/med/imagens/img195.gif) |
(4.1) |
e a transformada inversa, que recupera a função original é definida como:
![${\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty
F(w_x) e^{2i\pi w_xx} dw_x$](http://astro.if.ufrgs.br/med/imagens/img196.gif) |
(4.2) |
onde 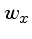 é a freqüência angular, e
é a freqüência angular, e 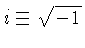 .
.
Para cada freqüência 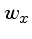 , integramos a função
, integramos a função 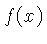 sobre todos os valores da coordenada
sobre todos os valores da coordenada 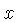 . Se o valor da integral for grande para esta freqüência, então o sinal tem uma componente significativa nesta freqüência, isto é, uma parte significativa deste sinal é composto por esta freqüência.
. Se o valor da integral for grande para esta freqüência, então o sinal tem uma componente significativa nesta freqüência, isto é, uma parte significativa deste sinal é composto por esta freqüência.
Podemos também definir:
![$ \boxed{{\cal{F}}[f(x)] \equiv F(\nu) = \int_{-\infty}^\infty f(x) e^{-i \nu x} dx,}$](http://astro.if.ufrgs.br/med/imagens/img201.gif) |
(4.3) |
e a transformada inversa, que recupera a função original é definida como :
![$ \boxed{{\cal{F}}^{-1}[F(\nu)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(\nu) e^{i\nu x} d\nu,}$](http://astro.if.ufrgs.br/med/imagens/img202.gif) |
(4.4) |
onde 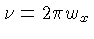 é a freqüência linear.
é a freqüência linear.
Note que:
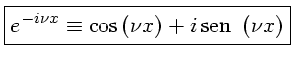
A condição suficiente para e existência da transformada de Fourier de uma função 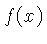 qualquer é que a função seja integrável, e finita, isto é:
qualquer é que a função seja integrável, e finita, isto é:
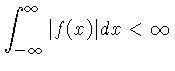 |
(4.5) |
As medidas e imagens que estamos interessados são sempre integráveis e finitas.
Embora a imagem seja real, a transformada de Fourier é uma função complexa, com coeficientes reais e imaginários:
![$ \boxed{F(w_x) = \Re[F(w_x)] + i\Im[F(w_x)].}$](http://astro.if.ufrgs.br/med/imagens/img207.gif)
O espectro de potências 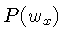 é definido como:
é definido como:
![$ \boxed{P(w_x) = \Re[F(w_x)]^2 + \Im[F(w_x)]^2,}$](http://astro.if.ufrgs.br/med/imagens/img209.gif)
e o ângulo de fase é dado por:
![$ \boxed{\phi(w_x)=\tan^{-1} \frac {\Im[F(w_x)]}{\Re[F(w_x)]}.}$](http://astro.if.ufrgs.br/med/imagens/img210.gif)
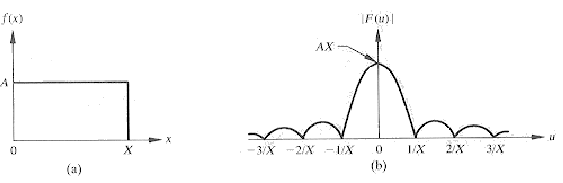
Por exemplo, podemos calcular a transformada de Fourier de um pulso retangular, definido por:
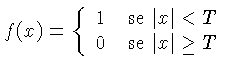
A transformada de Fourier 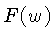 de
de 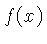 é dada por:
é dada por:
![$ {\cal{F}}[f(x)] \equiv F(w)$](http://astro.if.ufrgs.br/med/imagens/img213.gif) |
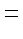 |
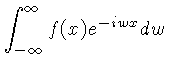 |
|
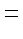 |
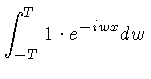 |
||
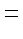 |
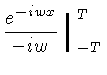 |
||
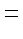 |
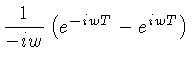 |
||
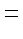 |
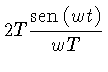 |
||
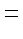 |
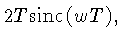 |
já que
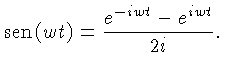
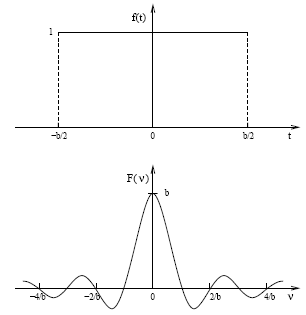
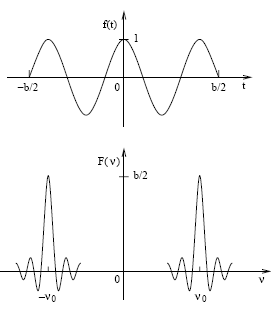
Transformada de Fourier de uma função caixa (um pulso retangular).
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
1) A Transformada de Fourier Discreta − tempo/frequência discreta (normalmente, conhecida apenas como Transformada Discreta de Fourier ou Discr...
Engenharia Eletrônica Integrada
•FADERGS
HARNISCH







Compartilhar