DETERMINE A DIMENSÃO DO SUBESPAÇO DE R^3 GERADO PELOS VETORES {(1,0,2),(3,1,1),(9,4,-2),(-7,-3,2)}
💡 4 Respostas
igor felipe
dim= 3
Andre Smaira
Neste exercício, serão aplicados os conhecimentos sobre espaços vetoriais para determinar a dimensão do subespaço de 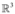
gerado pelos seguintes vetores:
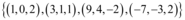
Com esses vetores, será montada a seguinte matriz:
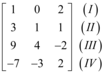
Agora, a matriz será reduzida pelo método do escalonamento. Para isso, serão realizadas operações entre as linhas. Essas operações são:
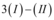
: para se obter uma nova linha 
;
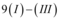
: para se obter uma nova linha 
;
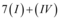
: para uma nova linha 
.
Com isso, a matriz resultante é:
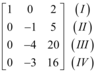
Agora, com as novas linhas, serão realizadas as seguintes operações:
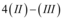
: para se obter uma nova linha 
;
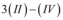
: para uma nova linha 
.
Com isso, a matriz resultante é:
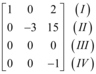
Nota-se que a linha 
(correspondente ao vetor 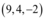
) foi completamente zerada. Isso significa que o vetor 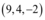
é resultado da combinação linear dos outros vetores.
Como a quantidade resultante de linhas não nulas é três, a dimensão procurada é igual a 
.
Concluindo, a dimensão do subespaço de 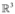
gerado pelos vetores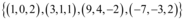
é igual a 
.
Andre Smaira
Neste exercício, serão aplicados os conhecimentos sobre espaços vetoriais para determinar a dimensão do subespaço de gerado pelos seguintes vetores:
Com esses vetores, será montada a seguinte matriz:
Agora, a matriz será reduzida pelo método do escalonamento. Para isso, serão realizadas operações entre as linhas. Essas operações são:
: para se obter uma nova linha ;
: para se obter uma nova linha ;
: para uma nova linha .
Com isso, a matriz resultante é:
Agora, com as novas linhas, serão realizadas as seguintes operações:
: para se obter uma nova linha ;
: para uma nova linha .
Com isso, a matriz resultante é:
Nota-se que a linha (correspondente ao vetor
) foi completamente zerada. Isso significa que o vetor
é resultado da combinação linear dos outros vetores.
Como a quantidade resultante de linhas não nulas é três, a dimensão procurada é igual a .
Concluindo, a dimensão do subespaço de gerado pelos vetores
é igual a
.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Materiais relacionados
 1 pág.
1 pág. 2 pág.
2 pág.




Compartilhar