A função f(x)=5x/x^2+3 é o comportamento de um escoamento unidimensional de um fluido ideal num intervalo {-1,1]. Determine a integral dessa função.

Para fazer o cálculo desta integral é necessário saber a substituição u. du, que consiste em mudar a variável x para uma nova variável u, integrando em função de u e substituindo para a variável original, que é x.  Após isto, usaremos o teorema fundamental do cálculo(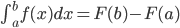) para calcular o valor nos limites de integração.

A integral do problema:

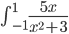
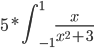 Deslocamento da constante, 

Substituição u.du.

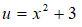
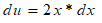
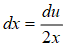
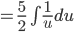Uso da integral básica,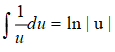 

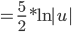 Substituindo de volta,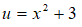 

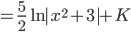
Calculando os limites de integração:

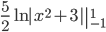
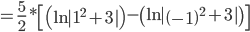
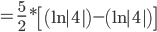
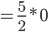
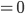
Portanto, a integral de 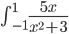 é .

Podemos resolver essa equação por isso de um integral simples.

Primeiro vamos montar a integral:

Vamos remover a contastante:

Aplicar integração por substituição:

Remover novamente a constante:

Aplicar a regra da integração:

Substituir na equação

E por fim simplicaficar e adcionar a constante: