COMO CALCULAR EDO DE SEGUNDA ORDEM?
💡 3 Respostas
Andre Smaira
As EDO’s de segunda ordem, lineares homogêneas, são da seguinte forma: 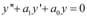 , onde
, onde  é a equação,
é a equação,  sua derivada primeira,
sua derivada primeira,  sua derivada segunda, e
sua derivada segunda, e 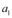 e
e 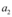 constantes.
constantes.
Substituindo-se  ,
,  e
e  na equação, deve-se obter a equação característica associada, a qual é da forma
na equação, deve-se obter a equação característica associada, a qual é da forma 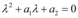 , tem raízes
, tem raízes 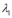 e
e 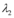 e:
e:
- Se
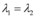 , sendo
, sendo 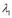 e
e 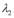 dois números reais, a solução geral da EDO é
dois números reais, a solução geral da EDO é 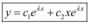 ;
; - Se
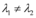 , sendo
, sendo 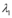 e
e 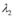 dois números reais,
dois números reais, 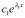 e
e 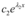 são soluções particulares da EDO, sendo sua solução geral
são soluções particulares da EDO, sendo sua solução geral 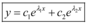 ; e
; e - Se
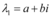 e
e 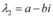 , sendo
, sendo  reais e
reais e 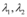 complexos conjugados, a solução geral da EDO é
complexos conjugados, a solução geral da EDO é 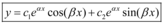 , onde
, onde  e
e 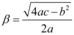 .
.
Para maior compreensão, façamos um exemplo. Seja 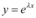 . Então, temos
. Então, temos 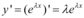 e
e 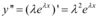 .
.
Substituindo na equação:

Assim, a equação característica associada à EDO será 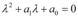 .
.
No caso de 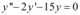 , temos a equação característica
, temos a equação característica 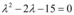 , cujas raízes são
, cujas raízes são  e
e 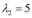 , de modo que, sendo
, de modo que, sendo 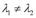 ,
,  e
e 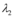 dois números reais, a solução geral será
dois números reais, a solução geral será 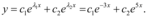
Andre Smaira
As EDO’s de segunda ordem, lineares homogêneas, são da seguinte forma: , onde
é a equação,
sua derivada primeira,
sua derivada segunda, e
e
constantes.
Substituindo-se ,
e
na equação, deve-se obter a equação característica associada, a qual é da forma
, tem raízes
e
e:
Se
, sendo
e
dois números reais, a solução geral da EDO é
;
Se
, sendo
e
dois números reais,
e
são soluções particulares da EDO, sendo sua solução geral
; e
Se
e
, sendo
reais e
complexos conjugados, a solução geral da EDO é
, onde
e
.
Para maior compreensão, façamos um exemplo. Seja . Então, temos
e
.
Substituindo na equação:
Assim, a equação característica associada à EDO será .
No caso de , temos a equação característica
, cujas raízes são
e
, de modo que, sendo
,
e
dois números reais, a solução geral será
RD Resoluções
As EDO’s de segunda ordem, lineares homogêneas, são da seguinte forma: , onde
é a equação,
sua derivada primeira,
sua derivada segunda, e
e
constantes.
Substituindo-se ,
e
na equação, deve-se obter a equação característica associada, a qual é da forma
, tem raízes
e
e:
Se
, sendo
e
dois números reais, a solução geral da EDO é
;
Se
, sendo
e
dois números reais,
e
são soluções particulares da EDO, sendo sua solução geral
; e
Se
e
, sendo
reais e
complexos conjugados, a solução geral da EDO é
, onde
e
.
Para maior compreensão, façamos um exemplo. Seja . Então, temos
e
.
Substituindo na equação:
Assim, a equação característica associada à EDO será .
No caso de , temos a equação característica
, cujas raízes são
e
, de modo que, sendo
,
e
dois números reais, a solução geral será
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Como calcular uma equacao direferencial de segunda ordem
Equações Diferenciais Ordinárias
•ESTÁCIO
Paulo Lima
Considere a seguinte equação diferencial de segunda ordem que descreve um sistema de oscilação: Um sistema de um pêndulo simples pode ser também ...
Equações Diferenciais Ordinárias
•MULTIVIX
Ryan Araújo
Materiais relacionados
 52 pág.
52 pág.




Compartilhar