Sejam u = (2, 0, −1) e v = (1, −1, 1) vetores do IR3 .
(a) Determine a projeção ortogonal de u sobre v (P rojvu)
(b) Calcule a distância entre os vetores u e v.
(c) Determine S o subespaço vetorial do IR3 gerado por u e v.
(d) Determine uma base ortogonal para S
(e) Verifique se se o vetor w = (1, 1, −2) ∈ S. (f) Faça um esboço do subespaço S.
💡 3 Respostas
paloma rodrigues
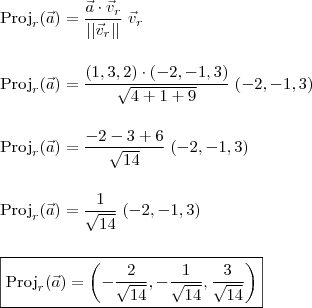
Acredito que está formula te ajude a resolver o primeiro item da questão é só substituir o a da fórmula por u.
Andre Smaira
São utilizados conceitos e relações de álgebra linear para obtenção dos itens pedidos.
- A projeção ortogonal de u sobre v é:
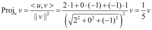
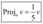
- A distância entre u e v é dada por
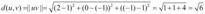
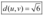
- O subespaço S gerado por u e v é denotado por:
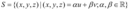
Temos então que,
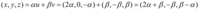
e, portanto,
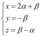
Utilizando a relação acima, temos que,
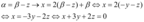
Portanto, o subespaço S gerado por u e v é descrito por:

- Uma base ortogonal para S pode ser definida escolhendo um vetor
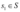 e encontrando um vetor
e encontrando um vetor  tal que
tal que 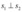 . Considerando o subespaço gerado S, pode-se verificar que
. Considerando o subespaço gerado S, pode-se verificar que 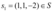 . Além disso, supondo um vetor
. Além disso, supondo um vetor 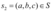 e
e 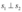 , então:
, então:
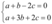
Somando as duas equações acima, encontramos que  . Assim,
. Assim,
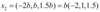
Portanto, os vetores 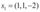 e
e  formam uma base ortogonal de S.
formam uma base ortogonal de S.
- Esse vetor foi utilizado como referência para a obtenção da base ortogonal no exercício anterior, portanto pertence ao subespaço S.
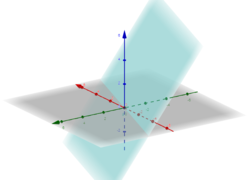
- Esboço do subespaço S:
RD Resoluções
São utilizados conceitos e relações de álgebra linear para obtenção dos itens pedidos.
A projeção ortogonal de u sobre v é:
A distância entre u e v é dada por
O subespaço S gerado por u e v é denotado por:
Temos então que,
e, portanto,
Utilizando a relação acima, temos que,
Portanto, o subespaço S gerado por u e v é descrito por:
Uma base ortogonal para S pode ser definida escolhendo um vetor
e encontrando um vetor
tal que
. Considerando o subespaço gerado S, pode-se verificar que
. Além disso, supondo um vetor
e
, então:
Somando as duas equações acima, encontramos que
. Assim,
Portanto, os vetores
e
formam uma base ortogonal de S.
Esse vetor foi utilizado como referência para a obtenção da base ortogonal no exercício anterior, portanto pertence ao subespaço S.
Esboço do subespaço S:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Seja o conjunto de vetores B= { ( 1 , 1 ) , ( 2 , − 1 ) } , uma base do R 2 .
Álgebra Linear I
•UNINTER
Joce matei
Materiais relacionados
 2 pág.
2 pág.





Compartilhar