integral indefinida

ajudou m uito

A integração de uma função consiste em determinar a área abaixo da curva dessa função. Para isso existem diversos métodos, sendo que nesse exercício será empregado o método da integração por partes.

No caso temos a seguinte integral indefinida:

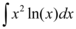
Segundo o método da integração por partes, sendo que u e v são duas funções independentes: 

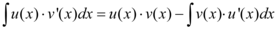
Se assumirmos que u e v são:

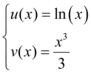
Então suas derivadas são:

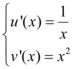
Logo, ao substituir tais variáveis na integral, temos:

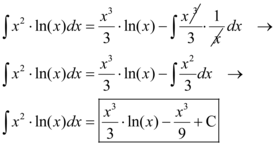
Onde C é a constante de integração para integrais indefinidas.

Portanto, pelo método da integração por partes, a integral enunciada possui a seguinte resposta:

¨

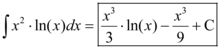
A resposta corresponde à alternativa A dentre as opções apresentadas.

Fonte: GUIDORIZZI, H. L.; Um Curso de Cálculo. Volume 2. 5ª edição, Rio de Janeiro, LTC, 2001.

A integração de uma função consiste em determinar a área abaixo da curva dessa função. Para isso existem diversos métodos, sendo que nesse exercício será empregado o método da integração por partes.

No caso temos a seguinte integral indefinida:

Segundo o método da integração por partes, sendo que u e v são duas funções independentes:

Se assumirmos que u e v são:

Então suas derivadas são:

Logo, ao substituir tais variáveis na integral, temos:

Onde C é a constante de integração para integrais indefinidas.

Portanto, pelo método da integração por partes, a integral enunciada possui a seguinte resposta:

A resposta corresponde à alternativa A dentre as opções apresentadas.

Fonte: GUIDORIZZI, H. L.; Um Curso de Cálculo. Volume 2. 5ª edição, Rio de Janeiro, LTC, 2001.