Calcule a integral de linha ∫xz ds onde C é a região é a interseção da esfera x²+y²+z²=9 com o plano z=(raiz quadrada de 5)
💡 4 Respostas
RD Resoluções
O calculo da integral de linha deve se restringir a região da curva solicitada pelo exercício sendo assim iniciaremos por tal, definindo então o espaço a ser analisado.
Considerando então a esfera
E o plano
E substituindo uma equação na outra, obtemos a seguinte curva a qual a integral pode ser calculada.
Correspondendo então a uma circunferência centrada na origem de raio igual a 2.
Assim podemos iniciar a resolução tendo em vista que o limite [0,2] será atribuído a tal integral no momento oportuno.
Então temos a integral definida por
Considerando ds como uma parte infinitesimal da curva calculada, podemos representar tal como hipotenusa da do triangulo formado entre as coordenadas x e y.
Assim sendo verificamos que ds pode ser simplificada como
Sendo g(x) a função que representa a curva a qual estamos limitando a integração da equação fornecida no enunciado, sendo ela.
Logo teremos por conseguinte
Substituído os resultados encontrados
Na integral a ser solucionada
Temos
Para resolver tal integral de maneira mais simples, usaremos um artificio de substituição onde
Logo então temos
Retornando a equação, dessa vez teremos
Simplificando a equação acima, teremos
Que por sua vez é integrável, e torna se
Para que possamos concluir a questão, nos resulta unicamente restaurar a variável substituída.
Sabendo então que o valor do intervalo a ser analisado no interior da curva corresponde a [0,2], iremos finalizar o processo de integração substituindo tais valores, como dito anteriormente no momento oportuno.
Simplificando ao máximo obtemos a resposta da integral de linha desta equação na curva de intercessão entre a esfera e o plano com o valor devido de
Carlos Apolinário
NÃO SEI MANO
Andre Smaira
O calculo da integral de linha deve se restringir a região da curva solicitada pelo exercício sendo assim iniciaremos por tal, definindo então o espaço a ser analisado.
Considerando então a esfera
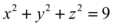
E o plano

E substituindo uma equação na outra, obtemos a seguinte curva a qual a integral pode ser calculada.
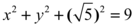
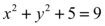
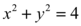
Correspondendo então a uma circunferência centrada na origem de raio igual a 2.
Assim podemos iniciar a resolução tendo em vista que o limite [0,2] será atribuído a tal integral no momento oportuno.
Então temos a integral definida por
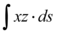
Considerando ds como uma parte infinitesimal da curva calculada, podemos representar tal como hipotenusa da do triangulo formado entre as coordenadas x e y.
Assim sendo verificamos que ds pode ser simplificada como
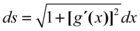
Sendo g(x) a função que representa a curva a qual estamos limitando a integração da equação fornecida no enunciado, sendo ela.
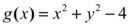
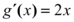
Logo teremos por conseguinte
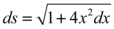
Substituído os resultados encontrados
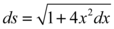

Na integral a ser solucionada
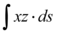
Temos
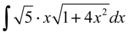
Para resolver tal integral de maneira mais simples, usaremos um artificio de substituição onde
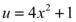
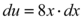
Logo então temos
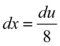
Retornando a equação, dessa vez teremos
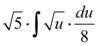
Simplificando a equação acima, teremos
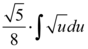
Que por sua vez é integrável, e torna se
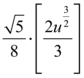
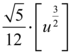
Para que possamos concluir a questão, nos resulta unicamente restaurar a variável substituída.
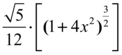
Sabendo então que o valor do intervalo a ser analisado no interior da curva corresponde a [0,2], iremos finalizar o processo de integração substituindo tais valores, como dito anteriormente no momento oportuno.
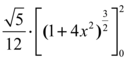
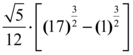
Simplificando ao máximo obtemos a resposta da integral de linha desta equação na curva de intercessão entre a esfera e o plano com o valor devido de
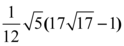
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta





Compartilhar