calculo 1

Área da lateral =\(2πRH\)         Área da base = \(πR^2\)       Volume = \(πR^2H\)

Volume = 1 \(m^2\) = \(πR^2H\)    →  \(H = 1/(R^2π)\)  em metro

\(C = \)(\(2πRH\)+\(πR^2\))1000 + (\(πR^2\))2000 = \({2000πR\over{R^2π} } + 1000πR^2 +2000πR^2\) = \({2000\over{R} } + 3000πR^2 \) 

sendo o R em metros e o custo em reais

v=r²**h

como volume é 1 m³

1=r²**h

h=1/(r²*)

o valor a pagar é :

C=2*r**1000+1000*r²*+2000*r²*

C=2*r**1000+3000*r²*

C=1651,47

derivada essa equação para saber o ponto critico(como é uma equação de grau 2 o ponto critico vai ser o minimo local, nesse caso)

\({dC \over dx}={-2 \over \pi²}*1000 +3000*2*\pi*r²\)

\(0={2000*(-1+3*\pi*r²) \over \pi²}\)

−1+3∗π∗r²=0

\(r= {1\over \sqrt{3*\pi}}\)

dai se subtituir esse valor na equação C deve dar o valor do custo minimo ,não sei se ta certo então é bom conferir se tem a resposta dessa questão.

C=2*\({1\over \sqrt{3*\pi}}\)**1000+3000*\( ({1\over \sqrt{3*\pi}})\)²*

Para resolver este problema, devemos colocar em prática nosso conhecimento sobre geometria, em especial sobre o volume e área de um cilindro.

Considerando que a caixa tenha a forma de um cilindro circular reto, seu volume será dado pela seguinte fórmula:

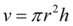
Em que V é o volume do cilindro, π é uma constante de valor aproximado a 3,14, r é o raio do cilindro e h a altura do cilindro.

A partir da equação do volume e do dado fornecido de que V = 1m3 podemos calcular a altura do cilindro.

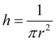
Em que h é a altura do cilindro, π é uma constante de valor aproximado a 3,14 e r é o raio do cilindro.

Para definirmos a expressão que representa o custo, devemos utilizar a formula da área do cilindro.

Área do cilindro = Área lateral + Área da tampa + Área do fundo

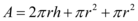
Substituindo h na formula da área do cilindro teremos:

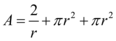
Em que A é a área do cilindro, π é uma constante de valor aproximado a 3,14 e r é o raio do cilindro.

A expressão que representa o custo será adquirida ao multiplicarmos cada área especifica do cilindro pelo respectivo custo do material.

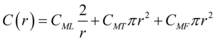
Em que C(r) é o custo em função do raio, π é uma constante de valor aproximado a 3,14, r é o raio do cilindro, CML é o custo do material da lateral, CMT  é o custo do material da tampa e CMF é o custo do material do fundo.

Substituindo na expressão os valores de CML, CMT e CMF que foram fornecidos no enunciado, definiremos então a expressão que representa o custo “C” do material utilizado em função do raio da base do cilindro.

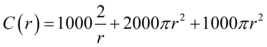
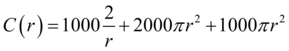
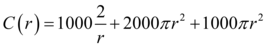
Em que C(r) é o custo em função do raio, π  é uma constante de valor aproximado a 3,14, r é o raio do cilindro.