calcule a derivada f(x)=x²-4x+20, no ponto x0=5, usando a definição de derivada atraves de um limite.
💡 4 Respostas
Albert Einstein

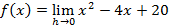
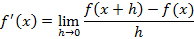
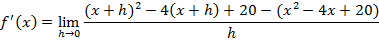
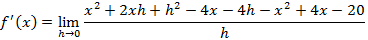
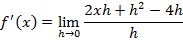
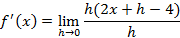
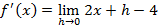

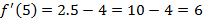
Espero ter ajudado. Se puder, curta minhas postagens e salve elas. Isso me ajudará a permanece PREMIUM. Bons estudos!
Andre Smaira
Contextualização:
Uma função f(x) definida em um intervalo aberto (a,b) é derivável no ponto 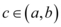 se existir o seguinte limite:
se existir o seguinte limite:
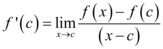
onde  representa a derivada de
representa a derivada de  .
.
Resolução:
Seja 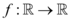 definida por
definida por 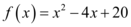 , temos no ponto
, temos no ponto  :
:
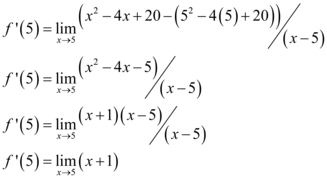
Sendo assim, temos:
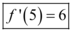
Conclusão:
Portanto, a derivada da função 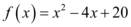 , no ponto
, no ponto 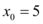 , usando a definição de derivada através de um limite é
, usando a definição de derivada através de um limite é  .
.
Andre Smaira
Contextualização:
Uma função f(x) definida em um intervalo aberto (a,b) é derivável no ponto se existir o seguinte limite:
onde representa a derivada de
.
Resolução:
Seja definida por
, temos no ponto
:
Sendo assim, temos:
Conclusão:
Portanto, a derivada da função , no ponto
, usando a definição de derivada através de um limite é
.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
f(x)=x² - 4x + 20, no ponto x0 = 5
Cálculo Diferencial e Integral A Uma Variável
•UNINTER
Kátia Vanessa





Compartilhar