Como responder essa questão?
Use o teorema de Rolle para provar que a equação:
x^5-5x^2+b=0 tem no máximo três raízes reais distintas, para todo valor de b.
💡 5 Respostas
Andre Smaira
Iniciaremos explicando a ideia do teorema em questão, o Teorema de Rolle é uma conjectura existencial, assim como o Teorema de Valor Médio.
O francês Michael Rolle (1652 - 1719) desenvolveu esse teorema com a intenção de afirmar a existencia de um dado externo considerando antes de tudo três condições principais.
No Teorema de Rolle temos a afirmação, dada uma função  na qual.
na qual.
- Seja continua em um dado intervalo fechado [a,b] ;
- Seja diferençável em todo intervalo aberto (a,b);
Tendo sido verificadas as duas condições acima citadas, e também.
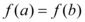
O teorema afirma que existe um ponto c tal qual.
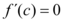
Verificando a função que foi dada:
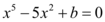
De acordo com o Teorema de Rolle sempre que houver duas raízes reais (R1, R2) sucessivas de um polinômio  de grau n, tem que haver uma raiz do polinômio
de grau n, tem que haver uma raiz do polinômio 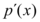 no mesmo intervalo. Isso facilita a análise das raízes, tendo em vista que um polinômio da função
no mesmo intervalo. Isso facilita a análise das raízes, tendo em vista que um polinômio da função 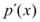 tem um grau menor que o da função original, fica evidentemente mais fácil a descoberta da mesma.
tem um grau menor que o da função original, fica evidentemente mais fácil a descoberta da mesma.
Assim sendo, temos a função
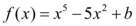
Realizando a derivada da função apresentada temos.
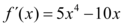
Considerando então que dentro do intervalo [a,b], exista um valor  = 0 como diz o Teorema de Rolle.
= 0 como diz o Teorema de Rolle.
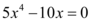
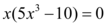
Podemos então verificar que uma das raízes reais dessa função é
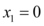
Seguindo com os termos não evidenciados
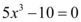
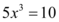
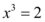
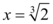
Definindo então as outras raízes possíveis como
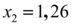
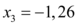
Assim podemos concluir que a função apresentada, para todo valor de b , tem ao menos 3 raízes possíveis.
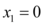
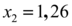
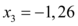
Andre Smaira
Iniciaremos explicando a ideia do teorema em questão, o Teorema de Rolle é uma conjectura existencial, assim como o Teorema de Valor Médio.
O francês Michael Rolle (1652 - 1719) desenvolveu esse teorema com a intenção de afirmar a existencia de um dado externo considerando antes de tudo três condições principais.
No Teorema de Rolle temos a afirmação, dada uma função na qual.
Seja continua em um dado intervalo fechado [a,b] ;
Seja diferençável em todo intervalo aberto (a,b);
Tendo sido verificadas as duas condições acima citadas, e também.
O teorema afirma que existe um ponto c tal qual.
Verificando a função que foi dada:
De acordo com o Teorema de Rolle sempre que houver duas raízes reais (R1, R2) sucessivas de um polinômio de grau n, tem que haver uma raiz do polinômio
no mesmo intervalo. Isso facilita a análise das raízes, tendo em vista que um polinômio da função
tem um grau menor que o da função original, fica evidentemente mais fácil a descoberta da mesma.
Assim sendo, temos a função
Realizando a derivada da função apresentada temos.
Considerando então que dentro do intervalo [a,b], exista um valor = 0 como diz o Teorema de Rolle.
Podemos então verificar que uma das raízes reais dessa função é
Seguindo com os termos não evidenciados
Definindo então as outras raízes possíveis como
Assim podemos concluir que a função apresentada, para todo valor de b , tem ao menos 3 raízes possíveis.
RD Resoluções
Iniciaremos explicando a ideia do teorema em questão, o Teorema de Rolle é uma conjectura existencial, assim como o Teorema de Valor Médio.
O francês Michael Rolle (1652 - 1719) desenvolveu esse teorema com a intenção de afirmar a existencia de um dado externo considerando antes de tudo três condições principais.
No Teorema de Rolle temos a afirmação, dada uma função na qual.
Seja continua em um dado intervalo fechado [a,b] ;
Seja diferençável em todo intervalo aberto (a,b);
Tendo sido verificadas as duas condições acima citadas, e também.
O teorema afirma que existe um ponto c tal qual.
Verificando a função que foi dada:
De acordo com o Teorema de Rolle sempre que houver duas raízes reais (R1, R2) sucessivas de um polinômio de grau n, tem que haver uma raiz do polinômio
no mesmo intervalo. Isso facilita a análise das raízes, tendo em vista que um polinômio da função
tem um grau menor que o da função original, fica evidentemente mais fácil a descoberta da mesma.
Assim sendo, temos a função
Realizando a derivada da função apresentada temos.
Considerando então que dentro do intervalo [a,b], exista um valor = 0 como diz o Teorema de Rolle.
Podemos então verificar que uma das raízes reais dessa função é
Seguindo com os termos não evidenciados
Definindo então as outras raízes possíveis como
Assim podemos concluir que a função apresentada, para todo valor de b , tem ao menos 3 raízes possíveis.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar