Como analisar uma curva de nível em uma paraboloide?
💡 3 Respostas
Andre Smaira
As superfícies de nível são formadas pelos gráficos de funções de três variáveis que seguem o seguinte formato:
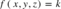
Onde k é uma constante previamente fixada que, geralmente, representa altura em um mapa de contorno.
Assim, unindo os pontos de mesma elevação na superfície de nível, obtemos assim uma função de duas variáveis no formato:
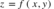
Desse modo, as curvas resultantes de funções deste tipo são chamadas de curvas de nível e, consequentemente, várias curvas de nível constituem um mapa de contorno.
As curvas de nível são utilizadas para verificar como uma das variáveis se modificam em relação a outra, mantendo a variável restante fixa.
Desse modo, para fazer os cálculos de curvas de nível, devemos assumir:
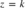
Assim, com um valor constante, encontramos o domínio da função e para cada valor associado a k substituído na função encontramos uma curva.
Desse modo, para parabolóides elípticos, basta realizar a análise da seguinte fórmula geral:
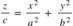
Já para parabolóides hiperbólicos, basta realizar a análise na seguinte fórmula:
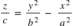
Onde a e b são constantes que determinam o grau de curvatura nos planos x-z e y-z e c é uma constante de variação de altura.
Andre Smaira
As superfícies de nível são formadas pelos gráficos de funções de três variáveis que seguem o seguinte formato:
Onde k é uma constante previamente fixada que, geralmente, representa altura em um mapa de contorno.
Assim, unindo os pontos de mesma elevação na superfície de nível, obtemos assim uma função de duas variáveis no formato:
Desse modo, as curvas resultantes de funções deste tipo são chamadas de curvas de nível e, consequentemente, várias curvas de nível constituem um mapa de contorno.
As curvas de nível são utilizadas para verificar como uma das variáveis se modificam em relação a outra, mantendo a variável restante fixa.
Desse modo, para fazer os cálculos de curvas de nível, devemos assumir:
Assim, com um valor constante, encontramos o domínio da função e para cada valor associado a k substituído na função encontramos uma curva.
Desse modo, para parabolóides elípticos, basta realizar a análise da seguinte fórmula geral:
Já para parabolóides hiperbólicos, basta realizar a análise na seguinte fórmula:
Onde a e b são constantes que determinam o grau de curvatura nos planos x-z e y-z e c é uma constante de variação de altura.
RD Resoluções
As superfícies de nível são formadas pelos gráficos de funções de três variáveis que seguem o seguinte formato:
Onde k é uma constante previamente fixada que, geralmente, representa altura em um mapa de contorno.
Assim, unindo os pontos de mesma elevação na superfície de nível, obtemos assim uma função de duas variáveis no formato:
Desse modo, as curvas resultantes de funções deste tipo são chamadas de curvas de nível e, consequentemente, várias curvas de nível constituem um mapa de contorno.
As curvas de nível são utilizadas para verificar como uma das variáveis se modificam em relação a outra, mantendo a variável restante fixa.
Desse modo, para fazer os cálculos de curvas de nível, devemos assumir:
Assim, com um valor constante, encontramos o domínio da função e para cada valor associado a k substituído na função encontramos uma curva.
Desse modo, para parabolóides elípticos, basta realizar a análise da seguinte fórmula geral:
Já para parabolóides hiperbólicos, basta realizar a análise na seguinte fórmula:
Onde a e b são constantes que determinam o grau de curvatura nos planos x-z e y-z e c é uma constante de variação de altura.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Determine o volume do sólido delimitado pelo paraboloide elíptico os planos
Cálculo Diferencial e Integral Aplicado II
•UNIASSELVI
Aparecido Rocha






Compartilhar