∭_r (e-(x^2+y^2+z^2))/√(x^2+y^2+x²) d V, em que T é solido limitado por duas esferas: x²+y²+z²=1 e x²+y²+z²=36

Ainda precisa da resolução?

sim. preciso

pessoal alguem pode me ajudar com as respostas dessas perguntas?

Calcule as integrais:

    a) 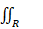    (x+y)dA, onde R é a região limitada por y = x²  e y=2x

    b) 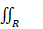     e – (x²+y²) dA, sendo R= {(x,y ) ϵ R²; 1 ≤x ² +y ² ≤ 4} 

   c) 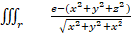    d V, em que T é solido limitado por duas esferas: x²+y²+z²=1 e x²+y²+z²=36