integrais duplas
Nos cálculos de integrais duplas, os limites de integração definem uma região D no plano XY. Essa região pode equivaler a um retângulo quando os limites são numéricos ou podem corresponder a outras figuras geométricas quando os limites de integração variam na forma de uma função.
Avalie as integrais e as regiões definidas abaixo:
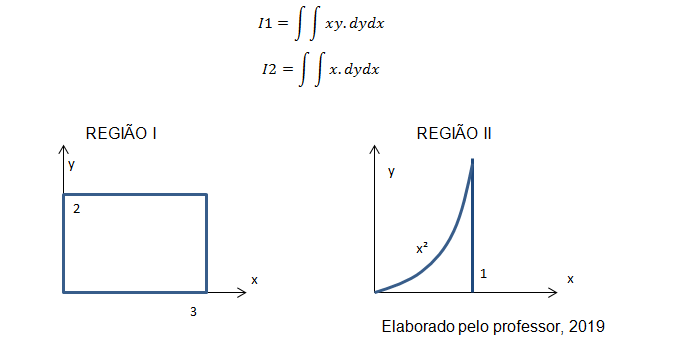
Sobre essas informações afirma-se:
I – A integral “I1” calculada na REGIÃO I é igual a 6.
II – A integral “I1” calculada na REGIÃO II é igual a 1/12.
III – A integral “I2” calculada na REGIÃO I é igual a 9.
IV – A integral “I2” calculada na REGIÃO II é igual a 1/4.
Estão corretas:
Alternativa 1:
Apenas II, III e IV.
Alternativa 2:
Apenas I, II e III.
Alternativa 3:
Apenas I e III.
Alternativa 4:
Apenas II e IV.
Alternativa 5:
I, II, III e IV.
💡 3 Respostas
Jeferson Correia
RD Resoluções
Nesse exercício vamos estudar integrais duplas.
Basicamente as afirmações são sobre os resultados de cada uma das integrais em cada uma das regiões, então vamos aos cálculos.
Para a primeira região, temos um retângulo em que $0<x<3$ e $0<y<2$, de forma que para a primeira integral temos:
$$I_{1,I}=\int_0^3\int_0^2xy\,dy\,dx$$
Integrando na variável interna, temos:
$$I_{1,I}=\int_0^3\left[\dfrac12xy^2\right]_0^2\,dx=\int_0^3\dfrac12x2^2\,dx=\int_0^32x\,dx$$
Agora integrando em $x$, temos:
$$I_{1,I}=\left[x^2\right]_0^3=9$$
Logo a afirmação I é falsa.
Para a mesma integral na segunda região, temos para os limites, que $0<x<1$ e $0<y<x^2$. Então para a integral em si, temos:
$$I_{1,II}=\int_0^1\int_0^{x^2}xy\,dy\,dx=\int_0^1\left[\dfrac12xy^2\right]_0^{x^2}\,dx =\dfrac12\int_0^1x^5\,dx$$
Agora integrando na segunda variável, temos:
$$I_{1,II} =\dfrac12\left[\dfrac16x^6\right]_0^1=\dfrac1{12}$$
Logo a afirmação II é verdadeira.
Agora vamos para a segunda integral em cada uma das regiões, começando pela região I:
$$I_{2,I}=\int_0^3\int_0^2x\,dy\,dx$$
Integrando na variável interna, temos:
$$I_{2,I}=\int_0^3\left[xy\right]_0^2\,dx=\int_0^32x\,dx$$
Agora integrando em $x$, temos:
$$I_{2,I}=\left[x^2\right]_0^3=9$$
Logo a afirmação III é verdadeira.
Por último vamos calcular a segunda integral na segunda região:
$$I_{2,II}=\int_0^1\int_0^{x^2}x\,dy\,dx=\int_0^1\left[xy\right]_0^{x^2}\,dx =\int_0^1x^3\,dx$$
Agora integrando na segunda variável, temos:
$$I_{2,II} =\left[\dfrac14x^4\right]_0^1=\dfrac14$$
Logo a afirmação IV é verdadeira.
Logo a Alternativa 1 é a correta.
Andre Smaira
Nesse exercício vamos estudar integrais duplas.
Basicamente as afirmações são sobre os resultados de cada uma das integrais em cada uma das regiões, então vamos aos cálculos.
Para a primeira região, temos um retângulo em que $0<x<3$ e $0<y<2$, de forma que para a primeira integral temos:
$$I_{1,I}=\int_0^3\int_0^2xy\,dy\,dx$$
Integrando na variável interna, temos:
$$I_{1,I}=\int_0^3\left[\dfrac12xy^2\right]_0^2\,dx=\int_0^3\dfrac12x2^2\,dx=\int_0^32x\,dx$$
Agora integrando em $x$, temos:
$$I_{1,I}=\left[x^2\right]_0^3=9$$
Logo a afirmação I é falsa.
Para a mesma integral na segunda região, temos para os limites, que $0<x<1$ e $0<y<x^2$. Então para a integral em si, temos:
$$I_{1,II}=\int_0^1\int_0^{x^2}xy\,dy\,dx=\int_0^1\left[\dfrac12xy^2\right]_0^{x^2}\,dx =\dfrac12\int_0^1x^5\,dx$$
Agora integrando na segunda variável, temos:
$$I_{1,II} =\dfrac12\left[\dfrac16x^6\right]_0^1=\dfrac1{12}$$
Logo a afirmação II é verdadeira.
Agora vamos para a segunda integral em cada uma das regiões, começando pela região I:
$$I_{2,I}=\int_0^3\int_0^2x\,dy\,dx$$
Integrando na variável interna, temos:
$$I_{2,I}=\int_0^3\left[xy\right]_0^2\,dx=\int_0^32x\,dx$$
Agora integrando em $x$, temos:
$$I_{2,I}=\left[x^2\right]_0^3=9$$
Logo a afirmação III é verdadeira.
Por último vamos calcular a segunda integral na segunda região:
$$I_{2,II}=\int_0^1\int_0^{x^2}x\,dy\,dx=\int_0^1\left[xy\right]_0^{x^2}\,dx =\int_0^1x^3\,dx$$
Agora integrando na segunda variável, temos:
$$I_{2,II} =\left[\dfrac14x^4\right]_0^1=\dfrac14$$
Logo a afirmação IV é verdadeira.
Logo a Alternativa 1 é a correta.
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Compartilhar