Qual a fórmula de bhaskara?
💡 6 Respostas
Robinson S Carvalho
A fórmula de Bhaskara é um método resolutivo para equações do segundo grau cujo nome homenageia o grande matemático indiano que a demonstrou. Essa fórmulanada mais é do que um método para encontrar as raízes reais de uma equação do segundo grau fazendo uso apenas de seus coeficientes. Vale lembrar que coeficiente é o número que multiplica uma incógnita em uma equação.
Em sua forma original, a fórmula de Bhaskara é dada pela seguinte expressão:
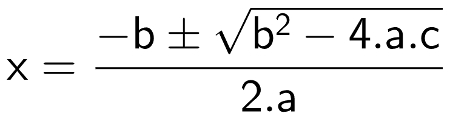
Andre Smaira
------
A Matemática trata-se de uma ciência lógica e abstrata focada no estudo de quantidades, medidas, espaços, estruturas, variações e estatísticas. O desenvolvimento da Matemática e seus conceitos teve início essencialmente na Mesopotâmia, no Egito e na Grécia. Em especial, após a Renascença a Matemática passou por uma grande evolução. Convém ressaltar que a mesma é de vital importância no cotidiano das pessoas e em praticamente qualquer área de trabalho.
---
Nesse contexto, a fórmula de Bhaskara, emprega para encontrar raízes de equações de segundo grau da forma a{x^2} + bx + c = 0\(\), está exposta abaixo:
\[\boxed{x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}}\]
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar