Sendo A e B?
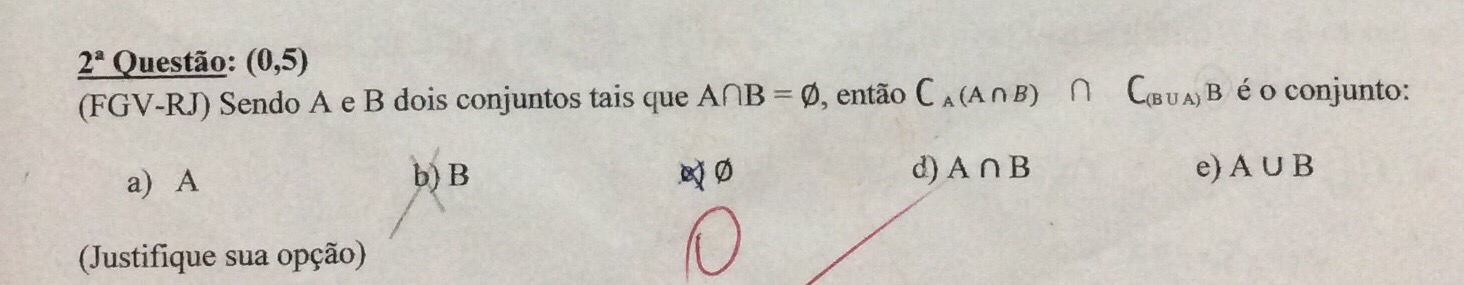
💡 5 Respostas
Andre Smaira
---
O exercício nos diz que:
\[A\cap B=\varnothing\]
Isto é, não há elementos na intersecção entre os conjuntos, ou, de forma mais simples, não existe nenhum elemento que pertença ao mesmo tempo a \(A\) e a \(B\).
---
Vamos determinar:
\[X=\complement_A(A\cap B)\cap \complement_{B\cup A}B\]
Vamos determinar cada parte dessa expressão independentemente. O símbolo \(\complement\) se refere ao complemento, de forma que \(\complement_AB\) significa o complemento de \(B\) em relação a \(A\), isto é, o conjunto dos elementos de \(A\) que não estão em \(B\).
\[\complement_A(A\cap B)=\{x|x\in A, x\notin A\cap B\}=\{x|x\in A, x\notin \varnothing\}=\{x|x\in A\}=A\]
\[\complement_{B\cup A}B=\{x|x\in B\cup A, x\notin B\}=\{x|x\in A\}=A\]
---
Voltando à expressão a ser calculada, temos:
\[X=\complement_A(A\cap B)\cap \complement_{B\cup A}B\]
\[X=A\cap A\]
---
Logo, a alternativa A é a correta:
\[\boxed{\complement_A(A\cap B)\cap \complement_{B\cup A}B=A}\]
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar