(a) Calcule o lado esquerdo. (b) Calcule o lado direito . (c) O que podemos concluir sobre o procedimento anterior? e justificando-as.
O Teorema de Stokes pode ser escrito como 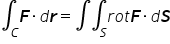 , ou seja, a integral de superfície do rotacional de um campo vetorial F sobre uma superfície S é igual a integral do campo vetorial F em alguma curva de fronteira C da superfície. Para essa questão discursiva considere o campo vetorial
, ou seja, a integral de superfície do rotacional de um campo vetorial F sobre uma superfície S é igual a integral do campo vetorial F em alguma curva de fronteira C da superfície. Para essa questão discursiva considere o campo vetorial 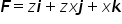 e a superfície S é formada pelo paraboloide
e a superfície S é formada pelo paraboloide 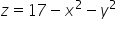 e o caminho C é o encontro entre o paraboloide e o plano
e o caminho C é o encontro entre o paraboloide e o plano 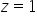 .
.
(a) Calcule o lado esquerdo do Teorema de Stokes.
(b) Calcule o lado direito do Teorema de Stokes.
(c) O que podemos concluir sobre o procedimento anterior?
Para os itens anterior, faça todos os cálculos necessários, mostrando todas as passagens e justificando-as.
💡 6 Respostas
Andre Smaira
a)
\[\eqalign{ & \int\limits_C {F*dr = \int {\int_S {rotF} *dS} } \cr & \int\limits_a {(\overrightarrow F \overrightarrow {dr} } ) \to \int\limits_a {(\overrightarrow F \overrightarrow {dr} } ) = \int\limits_{{a^b}} {(\overrightarrow F \overrightarrow {dr} } (t))*r'(t)dt \cr & r(t) = ? \cr & r(t):2 = 1;1 = 17 - {x^2} - {y^2} \cr & {x^2} + {y^2} = 16 \to r = 4 \to \{ (x = R\cos \theta ;y = R\sin \theta ;Z = Z) \cr & r(t) = (4\cos \,t,4\sin \,t,2) \cr & r'(t) = ( - 4\sin \,t,4\cos \,t,0) \cr & \int\limits_{t{i^{tf}}} {(\overrightarrow F (r(t))*r'(t)dt)} \cr & t(0,2\pi ) \cr & \overrightarrow F (r(t)) = (1,1*4\cos \,t,4\cos \,t) \cr & \int\limits_{t{i^{tf}}} {(1,4\cos )(t,} 4\cos (t)*( - 4\sin \,t,4\cos \,t(t,0)dt) \cr & ti = 0\,\,\,tf = 2\pi \cr & \int\limits_{{0^{2\pi }}} ( - 4\sin \,t\,\,dt + \int\limits_{{0^{2\pi }}} ( 16{(\cos \,)^2})t\,dt \to {(\cos )^{2x}} = {{(1 + \cos 2x)} \over 2} \cr & \int\limits_{{0^{2\pi }}} {\left( {{{16} \over 2}} \right)} dt + \int\limits_{{0^{2\pi }}} {\left( {{1 \over 2}} \right)} \cos \,2t)\,dt \to 8t = \int\limits_{{0^{2\pi }}} {( = 16)} }\]
b)
\[\eqalign{ & \int\limits_S {rot(\overrightarrow F )*(\overrightarrow {ds} ) = ?} \cr & Super.:z = 17 - {x^{2 - }} - {y^2} \to \{ (x = R\cos \theta y = R;\sin \theta Z = 1) \cr & \overrightarrow F = (Z,Zx,x) \cr & \theta = 0,2\pi \cr & Z(x,y) = 17 - {R^2}{(\cos \,)^2}\theta + {(\sin )^2}\theta ) = 17 - {R^2} \cr & R = 0,4 \cr & rot(\overrightarrow F )(i,j,k = {2 \over {2x}}{2 \over {2y}}{2 \over {2z}};z,zx,x) = ( - x,0,z) \cr & \overrightarrow {(ds)} = \overrightarrow {{r_R}} *\overrightarrow {{r_\theta }} (i,j,k = \cos \theta ,\sin \theta - R\sin \theta ,R\cos \theta ,0) = (0,0,R) \cr & \overrightarrow {{r_R}} = {{(\overrightarrow {dr} )} \over {dR}} = (\cos \theta ,\sin \theta ,0) \cr & \overrightarrow {{r_\theta }} = {{(\overrightarrow {dr} )} \over {d\theta }} = ( - Rsin\theta ,Rcos\theta ,0) \cr & \int {\int\limits_S {(( - R\sin \theta ,0,1)(0,0,R)dR\,d\theta } } \cr & \int\limits_{{0^{2\pi }}} {\int\limits_{{0^4}} {(Rdrd\theta = 2\pi *{{{R^2}} \over 2}} } ) \to {I_{{0^4}}} = 16\pi \cr & \int {\int\limits_S {((rot\overrightarrow R )*\,\overrightarrow {ds} } } = 16\pi }\]
c) Desse modo, conforme as demonstrações o Teorema de Stokes foi efetuado.
Fabricio Rodrigues
O Teorema de Stokes pode ser escrito como , ou seja, a integral de superfície do rotacional de um campo vetorial F sobre uma superfície S é igual a integral do campo vetorial F em alguma curva de fronteira C da superfície. Para essa questão discursiva considere o campo vetorial
e a superfície S é formada pelo paraboloide
e o caminho C é o encontro entre o paraboloide e o plano
.
(a) Calcule o lado esquerdo do Teorema de Stokes.
(b) Calcule o lado direito do Teorema de Stokes.
(c) O que podemos concluir sobre o procedimento anterior?
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 4 pág.
4 pág.



Compartilhar