Como achar equaçao reduzida da hiperbole?

Se os focos da hipérbole estiverem no eixo xx e seu centro for a origem, a equação reduzida da hipérbole é a seguinte:

x2a2−y2b2=1x2a2−y2b2=1

Em que aa é a medida do semieixo real e bb a medida do semieixo imaginário.

Se os focos estiverem no eixo yy então temos:

y2a2−x2b2=1y2a2−x2b2=1

Obs.: na hipérbole não é necessário que aa seja maior do que bb. Então, ao bater o olho em uma equação, vamos saber qual o eixo real através dos sinais de x2x2 e de y2y2.

A dedução da equação reduzida da hipérbole é similar à da elipse.

7.1

Exemplo 1: como determinar a equação de uma hipérbole

Iremos determinar a equação reduzida da hipérbole mostrada abaixo, em que F1F1 e F2F2 são seus focos.

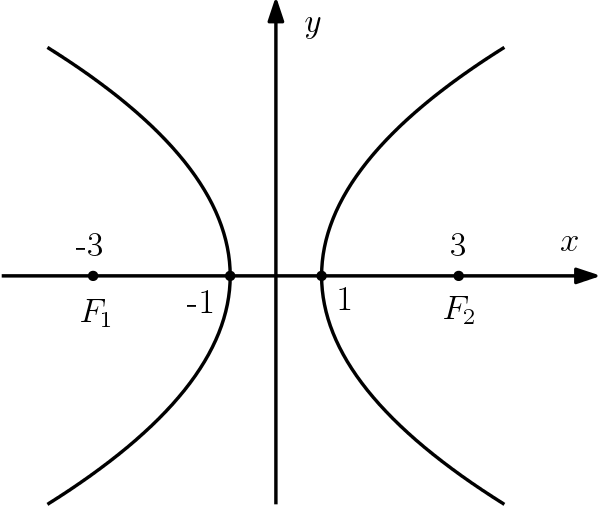
Pela figura podemos ver que a=1a=1 e que c=3c=3. Vamos utilizar a relação entre as medidas da hipérbole, pois precisamos de b2b2 para completar a equação:

c2=a2+b232=12+b29=1+b2b2=8c2=a2+b232=12+b29=1+b2b2=8

Portanto, a equação reduzida desta hipérbole será:

x2a2−y2b2=1x21–y28=1x2−y28=1

Pela definição de hipérbole, tem-se:

\[\left| {P{F_1} - P{F_2}} \right| = 2a\]

Assim:

\[\sqrt {{{\left( {x + c} \right)}^2} + {{\left( {y - 0} \right)}^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {{\left( {y - 0} \right)}^2}} = \pm 2a\]

\[\sqrt {{{\left( {x + c} \right)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{\left( {x - c} \right)}^2} + {{\left( {y - 0} \right)}^2}} \pm 2a\]

\[{\left( {x + c} \right)^2} + {y^2} = {\left( {x - c} \right)^2} + {y^2} \pm 4a\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + 4{a^2}\]

\[4cx - 4{a^2} = \pm 4a\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \Rightarrow cx - {a^2} = \pm a\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}\]

\[{\left( {cx - {a^2}} \right)^2} = {a^2}{\left( {x - c} \right)^2} + {a^2}{y^2}\]

\[{c^2}{x^2} - 2{a^2}cx + {a^4} = {a^2}{x^2} - 2{a^2}cx + {a^2}{c^2} + {a^2}{y^2}\]

\[\left( {{c^2} - {a^2}} \right){x^2} - {a^2}{y^2} = {a^2}\left( {{c^2} - {a^2}} \right)\]

Usando a relação notável da hipérbole \({c^2} = {a^2} + {b^2}\):

\[{b^2}{x^2} - {a^2}{y^2} = {a^2}{b^2}\]

Assim:

\[\boxed{\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1}\]

Por outro lado, se a hipérbole tiver os focos sobre o eixo \(y\), temos a seguinte relação:

\[\sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y + c} \right)}^2}} + \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - c} \right)}^2}} = \pm 2a\]

Donde a equação da hipérbole torna-se:

\[\boxed{\dfrac{{{y^2}}}{{{a^2}}} - \dfrac{{{x^2}}}{{{b^2}}} = 1}\]