1.Divida x³-a³ por x-a e conclua que x³-a³=(x-a)(x²+ax+a²). 2. Verifique as identidades.
a)\(x^2-a^2=(x-a)(x+a)\)
b)\(x^3-a^3=(x-a)(x^2+ax+a^2)\)
c)\(x^4-a^4=(x-a)(x^3+ax^2+a^2x+a^3)\)
d)\(x ^5-a^5=(x-a)(x^4+ax^3+a^2x^2+a^3x+a^4)\)
e)\(x ^n-a^n=(x-a)(x^{n-1}+ax^{n-2}+a^2x^{n-3}+...+a^{n-2}x+a^{n-1}) \)
em que n≠0 é um natural.
💡 1 Resposta
Lima Silva
Resolução do Livro "Um curso de cálculo" : Números Reais
Exercícios 1.2
1. Resolva a inequação.
Dica: Resolver inequações do 1° grau é simples :
1. Some os coeficientes de mesmo grau.
2. Isole a incógnita x em um dos membros da inequação.
a) 3x+3 < x+6
Solução:
3x+3 < x+6
3x -x < 6 -3
2x<3
x < 3/2

b) x-3 > 3x +1
Solução:
x-3 < 3x+1
x-3x < 1+3
-2x<4
2x > -4 *
x < -4/2
x < -2

c) 2x - 1 ≥ 5x + 3
Solução:
2x-1 ≥ 5x + 3
2x-5x ≥ 3+1
-3x ≥ 4
3x ≤ -4 *
x ≤ - 4/3

d) x+3 ≤ 6x-2
Solução:
x+3 ≤ 6x - 2
x - 6x ≤ -2 -3
-5x ≤ -5
5x ≥ 5 *
x ≥ 5/5
x ≥ 1

e) 1-3x > 0
Solução:
1-3x > 0
-3x >-1
3x < 1 *
x < 1/3
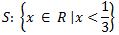
f) 2x +1 ≥ 3x
Solução:
2x +1 ≥ 3x
2x - 3x ≥-1
-x ≥ -1
x ≤ 1 *
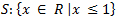
2. Estude o sinal da expressão.
Dica: Estudar o sinal de uma equação é determinar para que valores de x , a equação é nula, positiva ou negativa.
a) 3x-1
Solução:
Estudando o sinal de 3x - 1:
| 3x-1 < 0 3x < 1 x < 1/3 |
3x-1 = 0 3x = 1 x = 1/3 |
3x-1 > 0 3x > 1 x > 1/3 |
Graficamente:

Portanto,
- 3x - 1<0, para x < 1/3
- 3x - 1=0, para x = 1/3
- 3x - 1>0, para x > 1/3
b) 3-x
Solução:
Estudando o sinal de 3 - x:
| 3-x < 0 -x < -3 x > 3 * |
3-x = 0 -x = -3 x = 3 |
3-x > 0 -x > -3 x < 3 * |
Graficamente:

Portanto,
- 3 - x < 0, para x > 3
- 3 - x = 0, para x = 3
- 3 - x > 0, para x < 3
c) 2-3x
Solução:
Estudando o sinal de 2 - 3x:
| 2 - 3x< 0 -3x < -2 3x > 2 * x > 2/3 |
2 - 3x= 0 -3x = -2 3x = 2 x = 2/3 |
2 - 3x> 0 -3x >-2 3x < 2 * x < 2/3 |
Graficamente:

Portanto,
- 2 - 3x < 0, para x > 2/3
- 2 - 3x = 0, para x = 2/3
- 2 - 3x > 0, para x < 2/3
d) 5x+1
Solução:
Estudando o sinal de 5x + 1:
| 5x + 1< 0 5x < -1 x < -1/5 |
5x + 1< 0 5x < -1 x < -1/5 |
5x + 1< 0 5x < -1 x < -1/5 |
Graficamente:

Portanto,
- 5x + 1 < 0, para x < -1/5
- 5x + 1 = 0, para x = -1/5
- 5x + 1> 0, para x > -1/5
e) 
Solução:
Estudando o sinal de x-1:
| x - 1< 0 x <1 |
x - 1= 0 x =1 |
x - 1> 0 x >1 |
Estudando o sinal de x-2:
| x - 2< 0 x <2 |
x - 2= 0 x =2 |
x - 2> 0 x >2 |
Estudando o sinal de  :
:
- Se x-1 < 0 e x-2 < 0, logo
 >0 (- / - = +)
>0 (- / - = +) - Se x-1 >0 e x-2 <0 , logo <
 <0 (+/- = -)
<0 (+/- = -) - Se x-1 >0 e x-2 >0 , logo
 >0 (+ / + = +)
>0 (+ / + = +) - Se x - 1 =0 , logo
 = 0
= 0 - Se x-2 = 0, logo
 não estará definido! ( 1° mandamento da Matemática)
não estará definido! ( 1° mandamento da Matemática)
Graficamente:

Portanto,
 < 0, para 1 < x < 2
< 0, para 1 < x < 2 = 0, para x = 1
= 0, para x = 1 > 0, para x < 1 ou x > 2
> 0, para x < 1 ou x > 2 nao está definido em x = 2
nao está definido em x = 2
f) (2x + 1)(x - 2)
Solução:
Estudando o sinal de 2x + 1:
| 2x+1<0 2x<-1 x<-1/2 |
2x+1=0 2x=-1 x=-1/2 |
2x+1>0 2x>-1 x>-1/2 |
Estudando o sinal de x-2:
| x - 2< 0 x <2 |
x - 2= 0 x =2 |
x - 2> 0 x >2 |
Estudando o sinal de (2x + 1)(x - 2):
- Se 2x+1 < 0 e x-2 < 0, logo (2x + 1)(x - 2) > 0 (- x - = +)
- Se 2x+1 >0 e x-2 <0 , logo (2x + 1)(x - 2) < 0 (+ x - = -)
- Se 2x+1 >0 e x-2 >0 , logo (2x + 1)(x - 2) > 0 (+ x + = +)
- Se 2x+1 =0 ou x - 2 =0, logo (2x + 1)(x - 2) = 0
Graficamente:

Portanto,
- (2x+1)(x-2)< 0, para -1/2 < x < 2
- (2x+1)(x-2) = 0, para x = -1/2 ou x = 2
- (2x+1)(x-2)> 0, para x <-1/2 ou x > 2
g)
Solução:
Estudando o sinal de 2 - 3x:
| 2 - 3x< 0 -3x < -2 3x > 2 * x > 2/3 |
2 - 3x= 0 -3x = -2 3x = 2 x = 2/3 |
2 - 3x> 0 -3x >-2 3x < 2 * x < 2/3 |
Estudando o sinal de x+2:
| x + 2< 0 x < -2 |
x + 2= 0 x =-2 |
x + 2> 0 x > -2 |
Estudando o sinal de  :
:
- Se 2 - 3x > 0 e x+2 < 0, logo
 < 0 (+ / - = -)
< 0 (+ / - = -) - Se 2 - 3x >0 e x+2 >0 , logo
 > 0 (+/+ = +)
> 0 (+/+ = +) - Se 2 - 3x<0 e x+2 >0 , logo
 > 0 (- / + = -)
> 0 (- / + = -) - Se 2 - 3x =0 , logo
 = 0
= 0 - Se x+2 = 0, logo
 não estará definido! ( 1° mandamento da Matemática)
não estará definido! ( 1° mandamento da Matemática)
Graficamente:

Portanto,
 < 0, para x < -2 ou x > 2/3
< 0, para x < -2 ou x > 2/3 = 0, para x = 2/3
= 0, para x = 2/3 > 0, para -2 < x < 2/3
> 0, para -2 < x < 2/3 nao está definido em x = -2
nao está definido em x = -2
h)
Solução:
Estudando o sinal de 2 - x:
| 2 - x< 0 -x < -2 x > 2 * |
2 - x = 0 -x = -2 x = 2 |
2 - x> 0 -x > -2 x < 2 * |
Estudando o sinal de 3-x:
| 3 - x< 0 -x < -3 x >3* |
3 - x = 0 -x = -3 x = 3 |
3 - x> 0 -x > -3 x < 3* |
Estudando o sinal de  :
:
- Se 2 -x > 0 e 3-x > 0, logo
 > 0 (+ /+ = +)
> 0 (+ /+ = +) - Se 2 - x < 0 e 3-x > 0 , logo
 < 0 (-/+ = -)
< 0 (-/+ = -) - Se 2 - x<0 e 3-x <0 , logo
 > 0 (- / - = +)
> 0 (- / - = +) - Se 2 - x =0 , logo
 = 0
= 0 - Se 3 -x = 0, logo
 não estará definido! ( 1° mandamento da Matemática)
não estará definido! ( 1° mandamento da Matemática)
Graficamente:
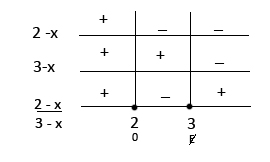
Portanto,
 < 0, para x < -2 ou x > 2/3
< 0, para x < -2 ou x > 2/3 = 0, para x = 2/3
= 0, para x = 2/3 > 0, para -2< x < 2/3
> 0, para -2< x < 2/3 nao está definido em x= -2
nao está definido em x= -2
i) (2x - 1)(3 - 2x)
Solução:
Estudando o sinal de 2x - 1:
| 2x-1<0 2x<1 x<1/2 |
2x-1=0 2x=1 x=1/2 |
2x-1>0 2x>1 x>1/2 |
Estudando o sinal de x-2:
| 3 - 2x< 0 -2x < -3 2x > 3 * x > 3/2 |
3 - 2x= 0 -2x = -3 2x = 3 x = 3/2 |
3 - 2x> 0 -2x > -3 2x < 3 * x < 3/2 |
Estudando o sinal de (2x - 1)(3 - 2x):
- Se 2x - 1 < 0 e 3 - 2x > 0, logo (2x - 1)(3 - 2x) >0 (- x + = -)
- Se 2x - 1 >0 e 3 - 2x >0 , logo (2x - 1)(3 - 2x)<0 (+ x + = +)
- Se 2x - 1 >0 e 3 - 2x <0 , logo (2x - 1)(3 - 2x) >0 (+ x - = -)
- Se 2x - 1 =0 ou 3 - 2x =0, logo (2x - 1)(3 - 2x) =0
Graficamente:

Portanto,
- (2x - 1)(3 - 2x)< 0, para x < 1/2 ou x > 3/2
- (2x - 1)(3 - 2x) = 0, para x = 1/2 ou x = 3/2
- (2x - 1)(3 - 2x)> 0, para 1/2 < x < 3/2
j) x(x - 3)
Solução:
Estudando o sinal de x - 3:
| x - 3<0 x < 3 |
x - 3=0 x = 3 |
x - 3>0 x > 3 |
Estudando o sinal de x(x - 3):
- Se x < 0 e x - 3< 0, logo x(x - 3) >0 (- x - = +)
- Se x >0 e x - 3 <0 , logo x(x - 3)<0 (+ x - = -)
- Se x >0 e x - 3 >0 , logo x(x - 3) >0 (+ x + = +)
- Se x =0 ou x - 3 =0, logo x(x - 3) =0
Graficamente:

Portanto,
- x(x - 3)< 0, para 0 < x < 3
- x(x - 3) = 0, para x = 0 ou x = 3
- x(x - 3)> 0, para x < 0 ou x > 3
l) x(x - 1)(2x + 3)
Solução:
Estudando o sinal de x-1:
| x - 1< 0 x <1 |
x - 1= 0 x =1 |
x - 1> 0 x >1 |
Estudando o sinal de 2x + 3:
| 2x + 3< 0 2x < -3 x <- 3/2 |
2x + 3= 0 2x = -3 x =- 3/2 |
2x + 3> 0 2x > -3 x >- 3/2 |
Estudando o sinal de x(x - 1)(2x + 3) :
- Se x <0 , x - 1<0 e 2x + 3 <0, logo x(x - 1)(2x + 3)
< 0 (- x -x -= -) - Se x<0 , x-1<0 e 2x+3 >0, logo (2x - 1)(3 - 2x)>0 (- x - x + = +)
- Se x >0 ,x - 1<0 e 2x + 3>0, logo (2x - 1)(3 - 2x) >0 (+ x - x += -)
- Se x >0 ,x - 1>0 e 2x + 3>0, logo (2x - 1)(3 - 2x) >0 (+ x + x += +)
- Se x =0 ,x - 1=0 e 2x + 3=0, logo (2x - 1)(3 - 2x) =0
Graficamente:

Portanto,
- x(x - 1)(2x + 3)< 0, para x < -3/2 ou 0 < x < 1
- x(x - 1)(2x + 3) = 0, para x = -3/2 , x = 0 ou x = 1
- x(x - 1)(2x + 3)> 0, para -3/2 < x < 0 ou x > 1
m) (x - 1)(1 + x)(2 - 3x)
Solução:
Estudando o sinal de x-1:
| x - 1< 0 x <1 |
x - 1= 0 x =1 |
x - 1> 0 x >1 |
Estudando o sinal de 1 + x:
| 1+x< 0 x < -1 |
1+x= 0 x = -1 |
1+x> 0 x > -1 |
Estudando o sinal de 2 - 3x:
| 2 - 3x< 0 -3x < -2 3x > 2 * x > 2/3 |
2 - 3x= 0 -3x = -2 3x = 2 x = 2/3 |
2 - 3x> 0 -3x >-2 3x < 2 * x < 2/3 |
Estudando o sinal de (x - 1)(1 + x)(2 - 3x) :
- Se x -1<0 , 1 + x<0 e 2 - 3x >0, logo(x - 1)(1 + x)(2 - 3x)
> 0 (- x -x + = +) - Se x - 1<0 , 1 + x>0 e 2 - 3x >0, logo (x - 1)(1 + x)(2 - 3x)<0 (- x + x + = -)
- Se x -1 <0 ,1 + x>0 e 2 - 3x<0, logo (x - 1)(1 + x)(2 - 3x) >0 (- x + x -= +)
- Se x -1 >0 ,1 + x>0 e 2 - 3x<0, logo (x - 1)(1 + x)(2 - 3x) <0 (+ x + x -= -)
- Se x -1 =0 ,1 + x=0 e 2 - 3x=0, logo (x - 1)(1 + x)(2 - 3x) =0
Graficamente:

Portanto,
- (x - 1)(1 + x)(2 - 3x)< 0, para -1 < x <2/3 ou x > 1
- (x - 1)(1 + x)(2 - 3x) = 0, para x = -1 , x = 2/3 ou x = 1
- (x - 1)(1 + x)(2 - 3x)> 0, para x < -1 ou 2/3 < x <1
n) x(x² + 3)
Solução:
Considerando que x² + 3 será sempre positivo, independente do valor de x, esse termo não influencia no estudo do sinal . Assim x determinará portanto o sinal da equação.
Graficamente:

Portanto,
- x(x² + 3)< 0, para x < 0
- x(x² + 3) = 0, para x = 0
- x(x² + 3)> 0, para x >0
o) (2x - 1)(x² + 1)
Solução:
Considerando que x² + 1 será sempre positivo, independente do valor de x, esse termo não influencia no estudo do sinal . Assim estudaremos somente o sinal de 2x-1, que determinará portanto o sinal da equação.
Estudando o sinal de 2x - 1:
| 2x-1<0 2x<1 x<1/2 |
2x-1=0 2x=1 x=1/2 |
2x-1>0 2x>1 x>1/2 |
Graficamente:

Portanto,
- (2x - 1)(x² + 1)< 0, para x < 1/2
- (2x - 1)(x² + 1) = 0, para x = 1/2
- (2x - 1)(x² + 1)> 0, para x >1/2
p) ax + b, onde a e b são reais dados, com a > 0.
Solução:
Estudando o sinal de ax + b, com a > 0:
| ax + b < 0 ax < -b x < -b/a |
ax + b = 0 ax = -b x = -b/a |
ax + b > 0 ax > -b x > -b/a |
Graficamente:

Portanto,
- ax+b<0, para x <-b/a
- ax+b=0, para x = -b/a
- ax+b>0, para x >-b/a
q) ax + b, onde a < 0 e b são dois reais dados.
Solução:
Vimos no exercicio anterior que a raiz da equação ax + b é -b/a, isto é, quando x = -b/a , ax + b = 0. Logo , no grafico a reta cruza o eixo x em -b/a. Considerandando que a < 0 , a função é decrescente. Veja o gráfico:

Portanto,
- ax+b<0, para x >-b/a
- ax+b=0, para x = -b/a
- ax+b>0, para x <-b/a
obs. Sendo f (x)=ax + b, sendo a e b dois reais dados , temos que o estudo do sinal de forma generica será:

3. Resolva a inequação.
Dica: Ao fazer o estudo do sinal podemos encontrar a solução da inequação facilmente. Observe que todas as funções que compõem as inequações são da forma ax + b, logo para fazer o estudo do sinal basta usar a fórmula genérica .

a) <0
<0
Solução:
Estudando o sinal de  :
:
1. Encontrando a raiz de 2x - 1:
2x-1 = 0
2x = 1
x=1/2
A raiz de 2x - 1 é 1/2.
2. Encontrando a raiz de x + 1:
x + 1 = 0
x = -1
A raiz de x + 1 é -1.
Graficamente:

Logo, <0 para -1 < x < 1/2.
<0 para -1 < x < 1/2.
b) ≥ 0
≥ 0
Solução:
Estudando o sinal de  :
:
1. Encontrando a raiz de 1 - x:
1 - x= 0
-x = -1
x=1
A raiz de 1 -x é 1.
2. Encontrando a raiz de 3 - x:
3 - x= 0
-x = -3
x=3
A raiz de 3 - x é 3.
Graficamente:

Logo, ≥ 0 para x ≤ 1 ou x > 3.
≥ 0 para x ≤ 1 ou x > 3.
c) >0
>0
Solução:
Estudando o sinal de  :
:
1. Encontrando a raiz de x - 2:
x - 2= 0
x = 2
A raiz de x - 2 é 2.
2. Encontrando a raiz de 3x + 1:
3x + 1= 0
3x = -1
x=-1/3
A raiz de 3x+1 é -1/3.
Graficamente:

Logo, > 0 para x < -1/3 ou x > 2
> 0 para x < -1/3 ou x > 2
d) (2x -1)(x+ 3)<0
Solução:
Estudando o sinal de (2x -1)(x+ 3):
1. Encontrando a raiz de 2x-1:
2x - 1= 0
2x = 1
x = 1/2
A raiz de 2x-1 é 1/2.
2. Encontrando a raiz de x + 3:
x + 3= 0
x = -3
A raiz de x + 3 é -3.
Graficamente:

Logo,(2x -1)(x+ 3)<0 para -3 < x < 1/2
e) ≤0
≤0
Solução:
Estudando o sinal de  :
:
1. Encontrando a raiz de 3x - 2:
3x - 2= 0
3x = 2
x=2/3
A raiz de 3x - 2 é 2/3.
2. Encontrando a raiz de 2-x:
2-x = 0
-x = -2
x = 2
A raiz de 2-x é 2.
Graficamente:

Logo, ≤ 0 para x ≤ 2/3 ou x > 2
≤ 0 para x ≤ 2/3 ou x > 2
f) x(2x - 1) ≥ 0
Solução:
Estudando o sinal de x(2x - 1):
1.A raiz de x é 0.
2. Encontrando a raiz de 2x - 1:
2x - 1= 0
2x = 1
x = 1/2
A raiz de 2x - 1 é 1/2.
Graficamente:

Logo, x(2x - 1) ≥ 0 para x ≤ 0 ou x ≥ 1/ 2
g) (x - 2)(x + 2) > 0
Solução:
Estudando o sinal de (x - 2)(x + 2):
1. Encontrando a raiz de x-2:
x-2= 0
x = 2
A raiz de x-2 é 2.
2. Encontrando a raiz de x + 2:
x + 2= 0
x = -2
A raiz de x + 2 é -2.
Graficamente:

Logo,(x - 2)(x + 2) > 0 para x < -2 ou x > 2
h)  > 5
> 5
Solução:
Antes é necessário deixar a desigualdade em relação a 0.

Estudando o sinal de  :
:
1. Encontrando a raiz de -3x+14:
-3x+14= 0
-3x= -14
3x= 14
x = 14/3
A raiz de -3x+14 é 14/3.
2. Encontrando a raiz de x - 3:
x -3= 0
x = 3
A raiz de x - 3 é 3.
Graficamente:

Logo, >0 ⇔
>0 ⇔  > 5 para 3 < x < 14/3.
> 5 para 3 < x < 14/3.
i)  ≤ 3
≤ 3
Solução:
Antes é necessário deixar a desigualdade em relação a 0.

Estudando o sinal de  :
:
1. Encontrando a raiz de -5x+9:
-5x+9= 0
-5x= -9
5x= 9
x = 9/5
A raiz de -5x+9 é 9/5.
2. Encontrando a raiz de 2x - 3:
2x -3= 0
2x= 3
x = 3/2
A raiz de 2x - 3 é 3/2.
Graficamente:

Logo, ≤ 0 ⇔
≤ 0 ⇔  ≤ 3 para x < 3/2 ou x ≥ 9/5
≤ 3 para x < 3/2 ou x ≥ 9/5
j) < 1
< 1
Solução:
Antes é necessário deixar a desigualdade em relação a 0.

Estudando o sinal de  :
:
1. Encontrando a raiz de 2x-3:
2x-3= 0
2x= 3
x= 3/2
A raiz de 2x-3 é 3/2.
2. Encontrando a raiz de 2-x:
2-x= 0
-x=-2
x = 2
A raiz de 2-x é 2.
Graficamente:

Logo, < 0 ⇔
< 0 ⇔  < 1 para x < 3/2 ou x > 2
< 1 para x < 3/2 ou x > 2
l) x(2x - 1)(x + 1) > 0
Solução:
Estudando o sinal de x(2x - 1)(x + 1):
1. Encontrando a raiz de 2x - 1:
2x - 1= 0
2x = 1
x = 1/2
A raiz de 2x - 1 é 1/2.
2. Encontrando a raiz de x+1:
x+1 = 0
x = -1
A raiz de x+1 é -1.
Graficamente:

Logo, x(2x - 1)(x + 1) > 0 para -1 < x < 0 ou x > 1/2.
m) (2x - 1)(x - 3) > 0
Solução:
Estudando o sinal de (2x -1)(x- 3):
1. Encontrando a raiz de 2x-1:
2x - 1= 0
2x = 1
x = 1/2
A raiz de 2x-1 é 1/2.
2. Encontrando a raiz de x - 3:
x - 3= 0
x = 3
A raiz de x - 3 é 3.
Graficamente:

Logo,(2x - 1)(x - 3)> 0 para x < 1/2 ou x > 3
n) (2x - 3)(x² + 1) < 0
Solução:
Considerando que x² + 1 será sempre positivo, independente do valor de x, esse termo não influencia no estudo do sinal . Assim estudaremos somente o sinal de 2x-3, que determinará portanto o sinal da equação.
1. Encontrando a raiz de 2x - 3:
2x - 3= 0
2x = 3
x = 3/2
A raiz de 2x - 3 é 3/2.
Graficamente:

Logo,(2x - 3)(x² + 1) < 0 para x < 3/2.
o)  < 0
< 0
Solução:
Considerando que x² + 1 será sempre positivo, independente do valor de x, esse termo não influencia no estudo do sinal . Assim estudaremos somente o sinal de x-3, que determinará portanto o sinal da equação.
1. Encontrando a raiz de x - 3:
x - 3= 0
x = 3
A raiz de x - 3 é 3.
Graficamente:

Logo, < 0 para x < 3.
< 0 para x < 3.
4. Divida x³ - a³ por x-a e conclua que x³ - a³ = (x - a)(x² + ax + a²)
Dica: A divisão de um polinomio F(x) por um polinomio G(x):
1. Se o grau de F(x) < G(x).
- o quociente Q(x) será 0 e o resto R(x) será igual a F(x).
2. Se o grau de F(x) ≤ G(x).
- dividir o termo de maior grau de F(x) pelo de maior grau de G(x), obtendo assim o primeiro termo do quociente Q(x). Exemplo: 4x² / 2x = (4/2)(x²/x)=2x.
- multiplique esse termo do quociente pelo primeiro termo de G(x), e subtraia de F(x) e copie os demais termos de F(x).
- Repita esses passos até que o grau de F(x) seja menor que G(x), obtendo o resto R(x).
Assim como na divisão aritmética temos que : dividendo = (divisor x quociente) + resto, portanto na divisão do polinômio F(x) = G(x)Q(x) + R(x). Se R(x) = 0, a divisão é considerada exata. Para saber mais sobre divisões de polinômios, veja em: Divisão de Polinômios.
Solução:

Sendo F(x) = G(x)Q(x)+R(x), substituindo temos que: x³ - a³ = (x - a)(x² + ax + a²) Verificando: x³ - a³ = (x - a)(x² + ax + a²) x³ - a³ = x³+ax²+a²x-ax²-a²x-a³ x³-a³=x³-a³
5. Verifique as identidades.
a) x² - a² = (x - a)(x + a)
Solução:

Sendo F(x) = G(x)Q(x)+R(x), substituindo temos que: x² - a² = (x - a)(x + a)
b) x³ - a³ = (x - a)(x² +ax+ a²)
Solução:

Sendo F(x) = G(x)Q(x)+R(x), substituindo temos que: x³ - a³ = (x - a)(x² +ax+ a²)
c) x4 - a4 = (x - a)(x³ + ax² +a²x + a³)
Solução:

Sendo F(x) = G(x)Q(x)+R(x), substituindo temos que: x4 - a4 = (x - a)(x³ + ax² +a²x + a³)
d) x5 - a5 = (x - a)(x4 + ax³ +a²x² + a³x + a4)
Solução:

Sendo F(x) = G(x)Q(x)+R(x), substituindo temos que: x5 - a5 = (x - a)(x4 + ax³ +a²x² + a³x + a4)
e) xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , onde n ≠ 0 é um natural.
Solução:

Sendo F(x) = G(x)Q(x)+R(x), considerando que a raiz da equação, temos que R(x)=0, logo: xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1)
6. Simplifique.
a)
Solução:
Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x² - 1 = x² - 1² =(x - 1)(x + 1) Substituindo :

b) 
Solução:
Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x³ - 8 = x³ - 2³ =(x - 2)(x² + 2x + 4) x² - 4 = x² - 2² =(x - 2)(x + 2) Substituindo :

c) 
Solução:
Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: 4x² - 9 = (2x)² - 3² = (2x - 3)(2x + 3) Substituindo :

d) 
Solução:

obs: 1 - x = - ( x - 1 )
e) 
Solução:

Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x² - 1 = x² - 1² = (x - 1)(x + 1) Substituindo :

obs: 1 - x² = - ( x² - 1 )
f) 
Solução:

Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x² - 9 = x² - 3² = (x - 3)(x + 3) Substituindo :

obs: 9 - x² = - ( x² - 9 )
g) 
Solução:

obs: 5 - x = - ( x - 5 )
h) 
Solução:

obs: p - x = - ( x - p )
i) 
Solução:

Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x² - p² = (x - p)(x + p) Substituindo :
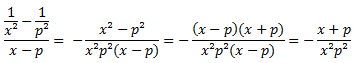
j) 
Solução:
Usando a formula geral xn - an = (x - a)(xn-1 + axn-2 + a²xn-3 + ... + an-2x + an-1) , temos que: x4 - p4 =(x - p)(x³ + px² + p²x + p³) Substituindo :

l) 
Dica: Veja as identidades dos produtos notáveis.
Solução:
Sabemos que :
( x + h )² = x² + 2hx + h² (produtos notáveis)
Substituindo:

m) 
Solução:

n) 
Dica: Veja as identidades dos produtos notáveis.
Solução:
Sabemos que :
( x + h )³ = x³ + 3hx² + 3h²x + h³ (produtos notáveis)
Substituindo:

o) 
Dica: Veja as identidades dos produtos notáveis.
Solução:
Sabemos que :
( x + h )² = x² + 2hx + h² (produtos notáveis)
( x - h )² = x² - 2hx + h² (produtos notáveis)
Substituindo:

7. Resolva a inequação.
Dica:
1. Estudo do sinal de expressões na forma ax² - c:
a) Encontrar as raízes x1 e x2 da equação:
ax² - c = 0
ax² = c
x² = c/a
x = ± √c/a
Portanto a equação terá duas raízes inteiras de mesmo módulo e sinais diferentes. Assim, x1= √c/a e x2= - √c/a.
b) Graficamente:
- Se a > 0 :
 ( Supondo x1 < x2 )
( Supondo x1 < x2 )
- Se a < 0:
 ( Supondo x1 < x2 )
( Supondo x1 < x2 )
2. Estudo do de expressões na forma ax + b:

a) x² - 4 > 0
Solução:
1. Estudo do sinal de x² - 4:
- Encontrar as raízes x1 e x2 da equação:
x² - 4 = 0
x² = 4
x = ± √4
x = ± 2
Assim, x1= -2 e x2= 2.
- Graficamente ( a > 0 ):

Logo, x² - 4 > 0 para x < -2 ou x > 2.
b) x² - 1 ≤ 0
Solução:
1. Estudo do sinal de x² - 1:
- Encontrar as raízes x1 e x2 da equação:
x² - 1 = 0
x² = 1
x = ± √1
x = ± 1
Assim, x1= -1 e x2= 1.
- Graficamente ( a > 0 ):

Logo, x² - 1 ≤ 0 para -1 ≤ x ≤ 1.
c) x² > 4
Solução:
Sabemos que x² > 4 ⇔ x² - 4 > 0, portanto a resolução é igual ao exercício a).
Logo, x² > 4 ⇔ x² - 4 > 0 para x < -2 ou x > 2.
d) x² > 1
Solução:
Sabemos que x² > 1 ⇔ x² - 1 > 0, portanto a resolução é igual ao exercício b).
Logo, x² >1⇔ x² - 1 > 0 para x < -1 ou x > 1.
e)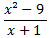 < 0
< 0
Solução:
Estudando o sinal de 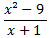 :
:
1. Estudo do sinal de x² - 9:
- Encontrar as raízes x1 e x2 da equação:
x² - 9 = 0
x² = 9
x = ± √9
x = ± 3
Assim, x1= -3 e x2= 3.
- Graficamente ( a > 0 ):

2. Estudo do sinal de x+1:
- Encontrar as raíz da equação:
x + 1= 0
x = -1
A raiz de x + 1 é -1.
- Graficamente :

Graficamente:

Logo,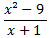 < 0 para x < -3 ou -1 < x < 3.
< 0 para x < -3 ou -1 < x < 3.
f)  >0
>0
Solução:
Considerando que x² + 4 será sempre positivo, independente do valor de x, esse termo não influencia no estudo do sinal . Assim estudaremos somente o sinal de x²-4, que determinará portanto o sinal da equação.
Veja o estudo do sinal de x²-4 em a).
Graficamente ( a > 0 ):

Logo, >0 para x < -2 ou x > 2.
>0 para x < -2 ou x > 2.
g) ( 2x - 1 )(x²- 4) ≤0
Solução:
Estudando o sinal de ( 2x - 1 )(x²- 4):
1. Estudo do sinal de 2x-1:
-Encontrar as raíz da equação:
2x-1= 0
2x= 1
x= 1/2
A raiz de 2x-1 é 1/2.
- Graficamente :

2. Veja o estudo do sinal de x²-4 em a):

Graficamente:

Logo,( 2x - 1 )(x²- 4) ≤ 0 para x ≤ -2 ou 1/2≤ x ≤2.
h) 3x² ≥ 48
Solução:
Sabemos que 3x² ≥ 48 ⇔ 3x² - 48 ≥ 0, portanto estudaremos o sinal de 3x²-48. 1.
Estudo do sinal de 3x²-48:
- Encontrar as raízes x1 e x2 da equação:
3x² - 48 = 0
3x² = 48
x² = 48/3
x² = 16
x = ± √16
x = ± 4
Assim, x1= -4 e x2= 4.
- Graficamente ( a > 0 ):

Logo, 3x² ≥ 48 ⇔ 3x² - 48 ≥ 0 para x ≤ -4 ou x ≥ 4 .
i) x² < r² , onde r > 0 é um real dado.
Solução:
Sabemos que x² < r² ⇔ x² - r² < 0, portanto estudaremos o sinal de x² - r².
1. Estudo do sinal de x² - r²:
- Encontrar as raízes x1 e x2 da equação:
x² - r² = 0
x² = r²
x = ± √r²
x = ± r
Assim, x1= -r e x2= r.
- Graficamente ( a > 0 ):

Logo, x² < r² ⇔ x² - r² < 0 para -r < x < r.
j) x² r² , onde r > 0 é um real dado.
Solução:
Sabemos que x² ≥ r² ⇔ x² - r² ≥ 0, portanto estudaremos o sinal de x² - r².
Veja o estudo do sinal de x² - r² em i).
Logo,x² ≥ r² ⇔ x² - r² ≥ 0 para x ≤ -r ou x ≥ 0 .
8. Considere o polinômio do 2° grau ax² + bx + c, onde a ≠ 0, b e c são reais dados.
a) Verifique que

Solução:

b) Conclua de (a) que , se Δ ≥ 0, as raízes de ax² + bx + c são dadas pela fórmula
Solução:
Dada a equivalência de a), temos:
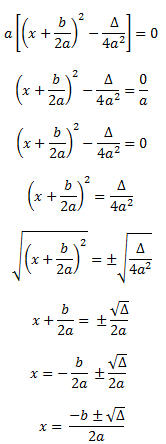
c) Sejam  e
e  (Δ ≥ 0) as raízes de ax² + bx + c. Verifique que
(Δ ≥ 0) as raízes de ax² + bx + c. Verifique que e
e  .
.
Solução:
-Substituindo x1 e x2 em x1 + x2, temos:

-Substituindo x1 e x2 em x1 x2, temos:

9. Considere o polinômio do 2° grau ax² + bx + c e sejam x1 e x2 como no item (c) do Exercicio. Verifique que
| ax² + bx + c = a(x - x1)(x - x2) |
Solução:
ax² + bx + c = a(x - x1)(x - x2)
ax² + bx + c = a(x² -x2x -x1x + x1x2)
ax² + bx + c = a( x² -x( x2 + x1 )+ x1x2 )
Como vimos no item (c) do exercício anterior  e
e 
Substituindo:

10. Utilizando o Exercício 9, fatore o polinômio do 2° grau dado.
Dica:
- Fatorando polinômios do tipo: ax² + bx + c:
- Encontrando as raízes x1 e x2 da equação:
 e
e  , onde Δ = b² - 4ac. portanto, ax² + bx + c = a(x-x1)(x-x2) - Trinômio Soma e Produto .
, onde Δ = b² - 4ac. portanto, ax² + bx + c = a(x-x1)(x-x2) - Trinômio Soma e Produto .
- Fatorando polinômios do tipo: ax² + bx :
Para fatorar polinômios desse tipo, basta colocar x em evidência. Assim, ax² + bx = x (ax + b) - Fator comum em evidência .
- Fatorando polinômios do tipo : ax² - c:
- Aplicando a regra dos produtos notáveis:
ax² - c = (√ax² + √c )(√ax² - √c) - Diferença entre dois quadrados
Para um estudo mais detalhado acesse : Fatoração de Polinômios.
a) x² - 3x +2
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-3)² - 4.1.2 Δ = 9 - 8 Δ = 1 |
  |
Portanto , x² - 3x +2 = ( x - 2)(x - 1).
b) x² - x - 2
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-1)² - 4.1.(-2) Δ = 1 + 8 Δ = 9 |
  |
Portanto , x² - x - 2 = ( x - 2)(x + 1).
c) x² - 2x + 1
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-2)² - 4.1.(1) Δ = 4-4 Δ = 0 |
Se Δ = 0 , temos x1 = x2 =  , logo: , logo: |
 |
Portanto , x² - 2x + 1 = ( x - 1)².
d) x² - 6x + 9
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-6)² - 4.1.9 Δ = 36-36 Δ = 0 |
Se Δ = 0 , temos x1 = x2 =  , logo: , logo: |
Portanto , x² - 6x + 9 = ( x - 3)².
e) 2x² - 3x
Solução:
Colocando x em evidência, temos 2x² - 3x = x (2x -3)
f) 2x² - 3x + 1
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-3)² - 4.2.1 Δ = 9 - 8 Δ = 1 |
  |
Portanto ,  .
.
g) x² - 25
Solução:
Aplicando a regra dos produtos notáveis:
x² - 25 = (√x² + √25 )(√x² - √25) = (x + 5)(x - 5)
h) 3x² + x - 2
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = 1² - 4.3.(-2) Δ = 1 + 24 Δ = 25 |
  |
Portanto ,
i) 4x² - 9
Solução:
Aplicando a regra dos produtos notáveis:
4x² - 9 = (2x)² - 3² = (2x - 3)(2x + 3).
j) 2x² - 5x
Solução:
Colocando x em evidência, temos 2x² - 5x = x (2x -5)
11. Resolva a inequação.
Dica: 1. Estudo do sinal de equações do 2° grau :
- 1° forma:
-Encontrar as raízes x1 e x2 da equação:
 e
e  , onde Δ = b² - 4ac.
, onde Δ = b² - 4ac.
-Graficamente:
Se a >0:
 ( Supondo x1 < x2 )
( Supondo x1 < x2 )
Se a < 0:
 ( Supondo x1 < x2 )
( Supondo x1 < x2 )
- 2° forma
-Encontrar as raízes x1 e x2 da equação:
 e
e  , onde Δ = b² - 4ac.
, onde Δ = b² - 4ac.
-Fatorar o polinômio: ax² + bx + c = a(x-x1)(x-x2)
-Fazer o estudo do sinal das expressões de 1° grau que compõem o produto a(x-x1)(x-x2).

a) x² - 3x + 2 < 0
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-3)² - 4.1.2 Δ = 9 - 8 Δ = 1 |
  |
-Graficamente (a > 0)

Logo x² - 3x + 2 < 0 , para 1 < x < 2 .
b) x² - 5x + 6 ≥ 0
Solução:
-Encontrando as raízes x1 e x2 da equação:
| Δ = (-5)² - 4.1.6 Δ = 25 - 24 Δ = 1 |
  |
-Graficamente (a > 0)

Logo x² - 5x + 6 ≥ 0 , para x ≤ 2 ou x ≥ 3.
c) x² - 3x > 0
Solução:
-Fatorando o polinômio:
x² - 3x = x (x - 3)
-Estudo do sinal de x (x - 3)
Encontrar a raiz de x - 3:
x-3 = 0
x = 3
-Graficamente:

Logo x² - 3x > 0 , para x < 0 ou x > 3.
d) x² - 9 < 0
Solução:
Encontrando as raízes x1 e x2 da equação:
x² - 9 = 0
x² = 9
x = ± √9
x = ± 3
Assim, x1= -3 e x2= 3.
Graficamente (a > 0)

Logo x² - 9 < 0 , para -3 < x < 3.
e) x² - x - 2 ≥ 0
Solução:
Encontrando as raízes x1 e x2 da equação:
| Δ = (-1)² - 4.1.(-2) Δ = 1 + 8 Δ = 9 |
  |
Graficamente (a > 0)

Logo x² - x - 2 ≥ 0, para x ≤ -1 ou x ≥ 2.
f) 3x² + x - 2 > 0
Solução:
Encontrando as raízes x1 e x2 da equação:
| Δ = 1² - 4.3.(-2) Δ = 1 + 24 Δ = 25 |
  |
Graficamente (a > 0)

Logo 3x² + x - 2 > 0, para x < -1 ou x > 2/3.
g) x² - 4x + 4 > 0
Solução:
Encontrando as raízes x1 e x2 da equação:
| Δ = (-4)² - 4.1.4 Δ = 16 -16 Δ = 0 |
Se Δ = 0 , temos x1 = x2 =  , logo: , logo: |
 |
Portanto , x² - 4x + 4 = ( x - 2)².
Considerando que ( x - 2)² será sempre positivo, independente do x, logo x² - 4x + 4 > 0, para todo x ≠2, pois (2 - 2)² = 0.
h) 3x² - x ≤ 0
Solução:
Fatorando o polinômio:
3x² - x = x (3x - 1)
Estudo do sinal de x (3x - 1)
- Encontrar a raiz de 3x - 1:
3x-1 = 0
3x=1
x=1/3
Graficamente:

Logo 3x² - x ≤ 0 , para 0 ≤ x ≤ 1/3.
i) 4x² - 4x + 1 < 0
Solução:
Encontrando as raízes x1 e x2 da equação:
| Δ = (-4)² - 4.4.1 Δ = 16 -16 Δ = 0 |
Se Δ = 0 , temos x1 = x2 =  , logo: , logo: |
Portanto , 4x² - 4x + 1 =  .
.
Considerando que  será sempre positivo, independente do x, logo 4x² - 4x + 1 < 0 , não adimite solução.
será sempre positivo, independente do x, logo 4x² - 4x + 1 < 0 , não adimite solução.
j) 4x² - 4x + 1 ≤ 0
Solução:
Vimos no item ( i ) que :
4x² - 4x + 1 =  .
.
Considerando que  será sempre positivo, independente do x,assim 4x² - 4x + 1 , não adimite solução para 4x² - 4x + 1 < 0, porém 4x² - 4x + 1 = 0, quando x = 1/2. Logo, 4x² - 4x + 1 ≤ 0 para x = 1/2.
será sempre positivo, independente do x,assim 4x² - 4x + 1 , não adimite solução para 4x² - 4x + 1 < 0, porém 4x² - 4x + 1 = 0, quando x = 1/2. Logo, 4x² - 4x + 1 ≤ 0 para x = 1/2.
12. Considere o polinômio do 2° grau ax² + bx + c e suponha que Δ < 0 . Utilizando o item (a) do Exercício 8, prove:
a) se a > 0, então ax² + bx + c > 0 para todo x. b) se a < 0, então ax² + bx + c < 0 para todo x.
Solução:
No item (a) do Exercício 8, vimos que:

Supondo Δ < 0 , a igualdade fica da seguinte maneira:
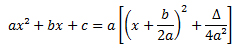
Fazendo  e
e  , constantes ∈ R, temos:
, constantes ∈ R, temos:
ax² + bx + c = a [ (x + d)² + e ]
Observe que (x + d)² + e será sempre positivo, portanto não influencia no sinal da equação, portanto , a determina o sinal da equação, assim:
- se a < 0 , a [ (x + d)² + e ] < 0 , portanto ax² + bx + c < 0.
- se a > 0, a [ (x + d)² + e ] > 0 , portanto ax² + bx + c > 0.
13. Resolva a inequação.
a) x² + 3 > 0
Solução:
Temos que: Δ = 0² - 4.1.3 = -12 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + 3 > 0 para todo x.
b) x² + x + 1> 0
Solução:
Temos que: Δ = 1² - 4.1.1 = -4 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + x + 1> 0 para todo x.
c) x² + x + 1 ≤ 0
Solução:
Temos que: Δ = 1² - 4.1.1 = -3 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + x + 1 ≤ 0 não adimite solução, pois x² + x + 1> 0 para todo x.
d) x² + 5 ≤ 0
Solução:
Temos que: Δ = 0² - 4.1.5 = -20 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + 5 ≤ 0 não adimite solução, pois x² + 5> 0 para todo x.
e) (x - 3)(x² + 5) > 0
Solução:
Estudando o sinal de (x - 3)(x² + 5):
1.Estudo do sinal de x - 3:
- Encontrando a raiz de x - 3:
x - 3= 0
x = 3
A raiz de x - 3 é 3.
2. Estudo do sinal de x² + 5:
Temos que: Δ = 0² - 4.1.5 = -20 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + 5> 0 para todo x. Assim o estudo do sinal é determinado por x - 3 , pois x² + 5 não influencia no estudo do sinal
Graficamente:

Logo,(x - 3)(x² + 5) > 0 para x > 3
f) (2x + 1)(x² + x + 1) ≤ 0
Solução:
Estudando o sinal de (2x + 1)(x² + x + 1):
1.Estudo do sinal de 2x + 1:
- Encontrando a raiz de 2x + 1:
2x + 1= 0
2x = -1
x = -1/2
A raiz de 2x + 1 é -1/2.
2. Estudo do sinal de x² + x + 1:
Temos que: Δ = 1² - 4.1.1 = -3 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + x + 1> 0 para todo x. Assim o estudo do sinal é determinado por 2x + 1 , pois x² + x + 1 não influencia no estudo do sinal
Graficamente:

Logo, (2x + 1)(x² + x + 1) ≤ 0, para x ≤-1/2
g) x(x² + 1 ) ≥ 0
Solução:
Estudando o sinal de x(x² + 1 ):
1.Estudo do sinal de x² + 1:
Temos que: Δ = 0² - 4.1.1 = -4 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + 1> 0 para todo x. Assim o estudo do sinal é determinado por x , pois x² + 1 não influencia no estudo do sinal
Graficamente:

Logo, x(x² + 1 ) ≥ 0, para x ≥ 0.
h) ( 1 - x)(x² + 2x + 2) < 0
Solução:
Estudando o sinal de ( 1 - x)(x² + 2x + 2):
1.Estudo do sinal de 1 - x:
- Encontrando a raiz de 1 - x:
1 - x= 0
-x = -1
x = 1
A raiz de 1 - x é 1.
2. Estudo do sinal de x² + 2x + 2:
Temos que: Δ = 2² - 4.1.2 = 4-8=-4 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior ,x² + 2x + 2> 0 para todo x. Assim o estudo do sinal é determinado por 1 - x , pois x² + 2x + 2 não influencia no estudo do sinal
Graficamente:
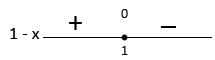
Logo, ( 1 - x)(x² + 2x + 2) < 0, para x > 1.
i) > 0
> 0
Solução:
Estudando o sinal de  :
:
1.Estudo do sinal de 2x-3:
- Encontrando a raiz de 2x-3:
2x-3= 0
2x = 3
x = 3/2
A raiz de 2x-3 é 3/2.
2.Estudo do sinal de x² + 1:
Temos que: Δ = 0² - 4.1.1 = -4 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + 1> 0 para todo x. Assim o estudo do sinal é determinado por 2x-3 , pois x² + 1 não influencia no estudo do sinal.
Graficamente:

Logo,  > 0, para x > 3/2.
> 0, para x > 3/2.
j)  ≥ 0
≥ 0
Solução: Estudando o sinal de  :
:
1.Estudo do sinal de x² + x + 1:
Temos que: Δ = 1² - 4.1.1 = 1-4 = -3 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício anterior , x² + x + 1> 0 para todo x. Assim o estudo do sinal é determinado por x , pois x² + x + 1 não influencia no estudo do sinal.
Graficamente:

Logo, ≥ 0, para x ≥ 0.
≥ 0, para x ≥ 0.
14. Prove :
 |
⇔ 5x + 3 ≥ 5 (x² + 1) |
Solução:
A equivalência só é verdadeira no intervalo em que x² + 1 > 0, pois quando multiplicamos os termos de uma inequação por um número negativo o sentido do sinal de desigualdade se inverte, o que tornaria a equivalência falsa.

Portanto, iremos fazer um estudo do sinal para descobrir o intervalo em que x² + 1 > 0.
1.Estudo do sinal de x² + 1:
Temos que: Δ = 0² - 4.1.1 = -4 < 0
Observe que Δ < 0 e a > 0, portanto de acordo com o exercício 12 , x² + 1> 0 para todo x. Logo, a sentença é válida para todo x.
15. A afirmação: "para todo x real , x ≠2
 |
⇔ x² + x + 1 > 3 (x - 2) |
é falsa ou verdadeira ? Justifique.
Solução:
A equivalência só é verdadeira no intervalo em que x-2 > 0, pois quando multiplicamos os termos de uma inequação por um número negativo o sentido do sinal de desigualdade se inverte, o que tornaria a equivalência falsa. Observe:
- Se x - 2 > 0

-Se x - 2 > 0

Portanto, iremos fazer um estudo do sinal para descobrir o intervalo em que x-2 > 0.
- Encontrar a raiz de x-2:
x-2 =0
x=2
- Graficamente :

Portanto a equivalência só é verdadeira no intervalo em que x > 2 , logo a afirmação é falsa.
16. Suponha que P(x) = a0xn + a1xn-1 + ... + an-1x + an seja um polinômio de grau n, com coeficiente inteiros, isto é, a0 ≠ 0, a1, a2, ... , an são números inteiros. Seja α um número inteiro. Prove que se α for raiz de P(x), então α será um divisor do termo independente an.
Solução:
Se α é raiz do polinômio, logo P(α) = 0. Assim :
a0αn + a1αn-1 + ... + an-1α + an= 0
an=- a0αn - a1αn-1 - ... - an-1α
an= α (- a0αn-1 - a1αn-2 - ... - an-1)
a n/ α = - a0αn-1 - a1αn-2 - ... - an-1
Fazendo k = - a0αn-1 - a1αn-2 - ... - an-1 , um inteiro. Temos :a n/ α = k
Logo, α é um divisor do termo independente an.
17. Utilizando o Exercício 16, determine, caso existam as raízes inteiras da equação.
Dica: Vimos no Exercicio 16 que a raiz do polinômio é um divisor do termo independente, portanto, faça teste com todas os divisores do termo independente.
a) x³ + 2x² + x - 4 = 0
Solução:
- Raízes possíveis: 1,-1,2,-2,4,-4.
- Testando:
P(1) = 1³ + 2.1 + 1 - 4 = 1 + 2 + 1 - 4 = 0 , portanto 1 é raíz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x-1):

Portanto, x³ + 2x² + x - 4 = (x - 1)(x²+3x+4)
-Encontrar as raízes de x²+3x+4:
Δ = 3² - 4.1.4 =9-16=-7 < 0
Logo, x²+3x+4 não possui raízes inteiras. Portanto o polinômio x³ + 2x² + x - 4 só possui uma raiz inteira: 1
b) x³ - x² + x + 14 = 0
Solução:
- Raízes possíveis: 1,-1,2,-2,7,-7,14,-14.
- Testando:
P(1) = 1³ -1² + 1+14=1-1+1+14 = 15
P(-1) = (-1)³ -(-1)²-1+14 = -1 - 1 -1 +14 = 11
P(2) = 2³ - 2² + 2 + 14 = 8 - 4 + 2 + 14 = 20
P(-2) = (-2)³ - (-2)² - 2 + 14 = -8 - 4 -2 +14 = 0 , portanto -2 é raiz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x+2):
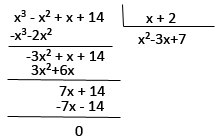
Portanto, x³ - x² + x + 14 = (x + 2)(x²-3x+7)
-Encontrar as raízes de x²-3x+7:
Δ = (-3)² - 4.1.7 =9-36=-25 < 0
Logo, x²-3x+7 não possui raízes inteiras.
Portanto o polinômio x³ - x² + x + 14 só possui uma raiz inteira: -2
c) x4 - 3x³ +x² + 3x = 2
Solução:
Sabendo que : x4 - 3x³ +x² + 3x = 2 ⇔ x4 - 3x³ +x² + 3x -2 = 0
Assim :
- Raízes possíveis: 1,-1,2,-2.
- Testando:
P(1) = 14 - 3.1³ +1² + 3.1 -2 = 1 - 3 +1 +3 -2 = 0 , portanto 1 é raiz da equação.
P(-1) = (-1)4 - 3.(-1)³ +(-1)² + 3.(-1) -2 = 1+3+1-3-2 = 0, portanto -1 é raiz da equação.
Descoberta duas raizes, podemos fatorar o polinômio para encontrar as demais raízes . Para isso divida o polinômio por (x-1), e depois divida o quociente por (x+1):
 |
 |
Logo, x4 - 3x³ +x² + 3x -2 = (x - 1)(x + 1)(x² - 3x+2) -Encontrar as raízes de x² - 3x +2:
| Δ = (-3)² - 4.1.2 Δ = 9 - 8 Δ = 1 |
  |
Assim , x² - 3x+2 = (x - 2)(x - 1)
Logo, x4 - 3x³ +x² + 3x -2 = (x - 1)²(x + 1)(x - 2)
Observe que o polinômio x4 - 3x³ +x² + 3x -2 possui raiz dupla 1.
Conclui-se que o polinomio x4 - 3x³ +x² + 3x -2 possui todas as raízes inteiras : 1,-1,2.
d) 2x³ - x² - 1 = 0
Solução:
- Raízes possíveis: 1,-1.
- Testando:
P(1) = 2.1³ - 1² - 1 = 2 - 1 -1 = 0 , portanto 1 é raiz da equação.
P(-1) = 2(-1)³ - (-1)² - 1 =-2 -1 -1= -4
Portanto 1 é raiz do polinômio 2x³ - x² - 1 .
e) x³ + x² + x - 14 = 0
Solução:
- Raízes possíveis: 1,-1,2,-2,7,-7,14,-14.
- Testando:
P(1) = 1³ + 1² + 1 - 14=1 + 1 + 1 - 14 = -11
P(-1) = (-1)³ + (-1)² + (-1) - 14 = -1 + 1 -1 -14 = -15
P(2) = 2³ + 2² + 2 - 14 = 8 + 4 + 2 - 14= 0 , portanto 2 é raíz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x-2):

Portanto, x³ + x² + x - 14 = (x - 2)(x²+3x+7)
-Encontrar as raízes de x²+3x+7:
Δ = 3² - 4.1.7 =9-36=-25 < 0
Logo, x²+3x+7 não possui raízes inteiras.
Portanto o polinômio x³ + x² + x - 14 só possui uma raiz inteira: 2.
f) x³ + 3x² - 4x -12 = 0
Solução:
- Raízes possíveis: 1,-1,2,-2,3,-3,4,-4,6,-6,12,-12.
- Testando:
P(1) = 1³ + 3.1² - 4.1 -12 = 1 + 3 -4 - 12 = -12
P(-1) = (-1)³ + 3(-1)² - 4(-1) -12 = -1 + 3 + 4 -12= -6
P(2) = 2³ + 3.2² - 4.2 -12 = 8 + 12 - 8 -12= 0 , portanto 2 é raíz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x-2):

Portanto, x³ + 3x² - 4x -12 = (x - 2)(x²+5x+6)
-Encontrar as raízes de x²+5x+6:
| Δ = 5² - 4.1.6 Δ = 25-24 Δ = 1 |
  |
Assim , x²+5x+6 = (x + 2)(x + 3)
Logo, x³ + 3x² - 4x -12 = (x - 2)(x + 2)(x + 3)
Conclui-se que o polinomio x4 - 3x³ +x² + 3x -2 possui todas as raízes inteiras : 2,-2,-3.
18. Seja P(x) um polinômio de grau n. Prove: α é raiz de P(x) ⇔ P(x) é divisível por x - α
Solução:
Dividindo P(x) por x - α , obtemos :
P(x) = (x - α) Q(x) + R(x)
Fazendo x = α , temos :
P(α) = (α - α) Q(α) + R(α)
P(α) = 0. Q(α) + R(α)
P(α) = R(α)
Sendo α raiz do polinômios, conclui-se que : P(α)=0 Se P(α) = R(α) , logo R(α) = 0, portanto P(x) é divisível por x - α.
19. Fatore o polinômio dado.
a) x³ + 2x² - x - 2
Solução:
- Raízes possíveis: 1,-1,2,-2.
- Testando:
P(1) = 1³ + 2.1² - 1 - 2 = 1+ 2 - 1 -2= 0 , portanto 1 é raiz da equação.
Descoberta uma raíz, iremos descobrir as demais dividindo o polinômio por (x-1):

Portanto, x³ + 2x² - x - 2 = (x - 1)(x²+3x+2)
Fatorandox²+3x+2 :
-Encontrar as raízes de x²+3x+2:
| Δ = 3² - 4.1.2 Δ = 9-8 Δ = 1 |
  |
Assim , x²+3x+2 = (x + 1)(x + 2)
Logo, x³ + 2x² - x - 2 = (x - 1)(x + 1)(x + 2)
b) x4 - 3x³ + x² + 3x - 2
Solução:
- Raízes possíveis: 1,-1,2,-2.
- Testando:
P(1) = 1 4 - 3.1³ + 1² + 3.1 - 2 = 1 -3 +1 +3 -2 = 0 , portanto 1 é raiz da equação.
Descoberta uma raíz, iremos descobrir as demais dividindo o polinômio por (x-1):

Portanto, x4 - 3x³ + x² + 3x - 2= (x - 1)(x³-2x²-x+2)
Vimos no item a) que : x³ + 2x² - x - 2 = (x - 1)(x + 1)(x + 2)
Logo, x4 - 3x³ + x² + 3x - 2= (x - 1)²(x + 1)(x + 2)
c) x³ + 2x² - 3x
Solução:
Fatorando por evidência, temos: x³ + 2x² - 3x = x ( x² + 2x -3)
Fatorando x² + 2x -3 :
-Encontrar as raízes de x² + 2x -3:
| Δ = 2² - 4.1.(-3) Δ = 4 + 12 Δ = 16 |
  |
Assim , x² + 2x -3 = (x - 1)(x + 3) Logo, x³ + 2x² - 3x = x (x - 1)(x + 3)
d) x³ + 3x² - 4x - 12
Solução:
- Raízes possíveis: 1,-1,2,-2.3,-3,4,-4,6,-6,12,-12.
- Testando:
P(1) = 1³ + 3.1² - 4.1 -12 = 1 + 3 -4 - 12 = -12
P(-1) = (-1)³ + 3(-1)² - 4(-1) -12 = -1 + 3 + 4 -12= -6
P(2) = 2³ + 3.2² - 4.2 -12 = 8 + 12 - 8 -12= 0 , portanto 2 é raíz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x-2):

Portanto, x³ + 3x² - 4x - 12= (x - 2)(x²+5x+6)
Fatorando x²+5x+6 :
-Encontrar as raízes de x²+5x+6:
| Δ = 5² - 4.1.6 Δ = 25-24 Δ = 1 |
  |
Assim , x²+5x+6 = (x + 2)(x + 3)
Logo, x³ + 3x² - 4x - 12 = (x - 2)(x + 2)(x + 3)
e) x³ + 6x² + 11x + 6
Solução:
- Raízes possíveis: 1,-1,2,-2.3,-3,6,-6.
- Testando:
P(1) = 1³ + 6.1² + 11.1 + 6 = 1 + 6 + 11 + 6 = 24
P(-1) = (-1)³ + 6(-1)² + 11(-1) + 6 = -1 + 6 - 11 + 6= 0 , portanto -1 é raiz da equação.
Descoberta uma raíz, iremos descobrir as demais fatorando o polinômio. Para isso divida o polinômio por (x+1):

Portanto, x³ + 6x² + 11x + 6 = (x + 1)(x²+5x+6)
Fatorando x²+5x+6 :
-Encontrar as raízes de x²+5x+6:
| Δ = 5² - 4.1.6 Δ = 25-24 Δ = 1 |
  |
Assim , x²+5x+6 = (x + 2)(x + 3)
Logo, x³ + 6x² + 11x + 6 = (x + 1)(x + 2)(x + 3)
f) x³ - 1
Solução:
- Raízes possíveis: 1,-1.
- Testando:
P(1) = 1³ - 1 = 0 , portanto 1 é raiz da equação.
Descoberta uma raíz, iremos descobrir as demais dividindo o polinômio por (x-1):

Portanto, x³ - 1 = (x - 1)(x² + x + 1)
-Encontrar as raízes de x² + x + 1:
Δ = 1² - 4.1.1 Δ = 1-4 Δ = - 3 < 0
Observe que x² + x + 1 não possui raízes reais, pois Δ< 0, logo x³ - 1 = (x - 1)(x² + x + 1).
20. Resolva a inequação.
a) x³ - 1 > 0
Solução:
Fatorando x³ - 1 , temos:
x³ - 1 = (x - 1)(x² + x + 1) - Veja no item (f) do Exercício 19.
Estudando o sinal de (x - 1)(x² + x + 1):
1.Estudo do sinal de x - 1:
- Encontrando a raiz de x - 1:
x - 1= 0
x = 1
A raiz de x - 1 é 1.
2. Estudo do sinal de x² + x + 1:
Temos que: Δ = 1² - 4.1.1 = 1-4=-3 < 0
Observe que Δ < 0 e a > 0, portanto x² + 2x + 2 > 0 para todo x.
Assim o estudo do sinal é determinado por x - 1 , pois x² + x + 1 não influencia no estudo do sinal
Graficamente:

Logo, x³ - 1 = (x - 1)(x² + x + 1) > 0, para x > 1.
b) x³ + 6x² + 11x + 6 < 0
Solução:
Fatorando x³ + 6x² + 11x + 6 , temos:
x³ + 6x² + 11x + 6 = (x + 1)(x + 2)(x + 3) - Veja no item (e) do Exercício 19.
Estudando o sinal de (x + 1)(x + 2)(x + 3):
1.Estudo do sinal de x - 1:
- Encontrando a raiz de x - 1:
x + 1= 0
x = -1
A raiz de x + 1 é -1.
2. Estudo do sinal de x + 2:
- Encontrando a raiz de x + 2:
x + 2= 0
x = -2
A raiz de x + 2 é -2.
3. Estudo do sinal de x + 3:
- Encontrando a raiz de x + 3:
x + 3= 0
x = -3
A raiz de x + 3 é -3.
Graficamente:

Logo, x³ + 6x² + 11x + 6 = (x + 1)(x + 2)(x + 3) < 0, para x < -3 ou -2 < x < -1.
c) x³ + 3x² - 4x - 12 ≥ 0
Solução:
Fatorando x³ + 3x² - 4x - 12 , temos: x³ + 3x² - 4x - 12 = (x - 2)(x + 2)(x + 3) - Veja no item (d) do Exercício 19.
Estudando o sinal de (x - 2)(x + 2)(x + 3):
1.Estudo do sinal de x - 2:
- Encontrando a raiz de x - 2:
x - 2= 0
x = 2
A raiz de x - 2 é 2.
2. Estudo do sinal de x + 2:
- Encontrando a raiz de x + 2:
x + 2= 0
x = -2
A raiz de x + 2 é -2.
3. Estudo do sinal de x + 3:
- Encontrando a raiz de x + 3:
x + 3= 0
x = -3
A raiz de x + 3 é -3.
Graficamente:

Logo, x³ + 3x² - 4x - 12 = (x - 2)(x + 2)(x + 3) ≥ 0, para -3 ≤ x ≤ -2 ou x ≥ 2 .
d) x³ + 2x² - 3x < 0
Solução:
Fatorando x³ + 2x² - 3x , temos: x³ + 2x² - 3x = x (x - 1)(x + 3) - Veja no item (c) do Exercício 19.
Estudando o sinal de x (x - 1)(x + 3):
1.Estudo do sinal de x - 1:
- Encontrando a raiz de x - 1:
x - 1= 0
x = 1
A raiz de x - 1 é 1.
2. Estudo do sinal de x + 3:
- Encontrando a raiz de x + 3:
x + 3= 0
x = -3
A raiz de x + 3 é -3.
Graficamente:

Logo, x³ + 2x² - 3x = x (x - 1)(x + 3) < 0, para x < -3 ou 0 < x < 1.
21. A afirmação : " quaisquer que sejam os reais x e y, x < y ⇔ x² < y² " é falsa ou verdadeira ? Justifique.
Solução:
É falsa. A afirmação somente é válida para x > 0 e y > 0 .
Observe que se x for negativo, porém maior em módulo do que y, teremos uma contradição :
Fazendo x = -2 e y = 3 , temos x² = 4 e y = 9 , logo x < y, porém x² > y².
22. Prove que quaisquer que sejam os reais x e y, x < y ⇔ x³ < y³.
Solução:
Sabemos que y > x , portanto faremos y = x + n , com n ∈N.
Assim ,
x³ < y³
x³ < (x + n)³
x³ < x³ + 3hx² + 3h²x + h³
Fazendo k = 3hx² + 3h²x + h³, temos:
x ³ < x³ + k
Portanto, x³ < y³
23. Neste exercício você deverá admitur como conhecidas apenas as propriedades (A1) a (A4), (M1) a (M4), (D), (O1) a (04), (OA) e (OM) . Supondo x e y quaisquer, prove:
a) x . 0 = 0
Solução:
Sabendo que :
x = x ⇔ x - x = 0
Fatorando , temos:
( 1 - 1)x =0
Por A4, obtemos:
0.x =0
b) (Regra dos sinais) (-x)y = -xy; x(-y)= -xy; (-x)(-y) = xy
Solução:
- Fatorando (-x)y , temos:
(-x)y = [( 1 - 2)x]y
Por D, obtemos:
[( 1 - 2)x]y = xy - 2xy = -xy
- Fatorando x(-y) , temos:
x(-y) = x[( 1 - 2)y]
Por D, obtemos:
x[( 1 - 2)y] = xy - 2xy = -xy
- Fatorando (-x)(-y) , temos:
(-x)(-y) = [( 1 - 2)x][( 1 - 2)y]
Por D, obtemos:
[( 1 - 2)x][( 1 - 2)y] = (x - 2x)(y - 2y) = xy - 2xy -2xy +4xy = xy - 4xy +4xy = xy
c) x² ≥ 0.
Solução: .
- Se x > 0
x² = x . x
Fatorando x.x, temos:
x.x = [(2-1)x][(2-1)x]
Por D, obtemos :
[(2-1)x][(2-1)x] = (2x - x)(2x - x) = 4x²-2x²-2x²+x² = 4x² - 4x² +x² = x²
- Se x < 0
(-x)² = (-x) .(-x)
Fatorando (-x) .(-x), temos:
(-x) .(-x) = [(1-2)x][(1-2)x]
Por D, obtemos :
[(1-2)x][(1-2)x] = (x - 2x)(x - 2x) = x² - 2x² -2x² +4x² = x² -4x² + 4² = x²
Logo x² > 0 , para todo x.
d) 1 > 0
Solução:
Seja 1 um número positivo. Se retirarmos um número maior de 1 , teriamos um número negativo. Vejamos :
1 - 0 = 1 > 0
Portanto 1 > 0.
e) x > 0 ⇔ x -1 > 0
Solução:
Se x -1< 0 , temos , por M4:
-(x -1)x = 1 > 0
Observe, que a multiplicação resultou em um número positivo. Veja em b, que a única situação em que isso é possivel é quando (-x)(-y) = xy > 0 , logo para x -1 > 0 , x > 0. Logo, o recíproco é verdadeiro.
f) (Anulamento do produto) xy = 0 ⇔ x=0 ou y=0
Solução:
Há três hipóteses :
-x ≠ 0 e y ≠ 0 :
Temos : xy = 0
Multiplicando x e y por seus respectivos inversos,logo:
(x -1.x)(y -1.y) = 0
Por M4, temos:
(x -1.x)(y -1.y) = 1
(Absurdo)
- x ≠ 0 e y = 0 :
Temos: xy = 0
Multiplicando x por seu respectivo inverso, temos:
(x -1.x).y = 0
Por M4, temos:
(x -1.x).y = 1.y = y.
Sendo y = 0, logo xy = 0
-x = 0 e y ≠ 0 :
Temos: xy = 0
Multiplicando y por seu respectivo inverso, temos:
x.(y -1.y) = 0
Por M4, temos:
x.(y -1.y) = x.1 = x.
Sendo x = 0, logo xy = 0
g) x² = y² ⇔ x = y ou x = -y
Solução:
Temos que :
x² = y² ⇔ x² - y² = 0
Fatorando :
x² - y² = 0
x² = y²
x = ± √y²
x = ± y
Logo, x² - y² = (x - y)(x+y) = 0
Fazendo m = x - y e n = x+y , temos : m.n = 0
Em (f), vimos que m.n = 0 ⇔ m=0 ou n=0.
Para m = 0 :
x - y = 0
x = y
Para n = 0:
x + y = 0
x = -y
Assim , se x² = y² ⇔ x = y ou x = -y
h) Se x ≥ 0 e y ≥ 0, x² = y² ⇔ x = y
Solução:
Idem a (g) , mas considerando que x ≥ 0 e y ≥ 0 , logo a expressão x = -y não é válida. Assim x² = y² se x = y.
______________________________________
* Ao multiplicarmos ambos os lados por um número negativo o sinal de desigualdade se invertee. Veja: - 3x < 5
-3x (-1) < 5 (-1)
3x > -5
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar