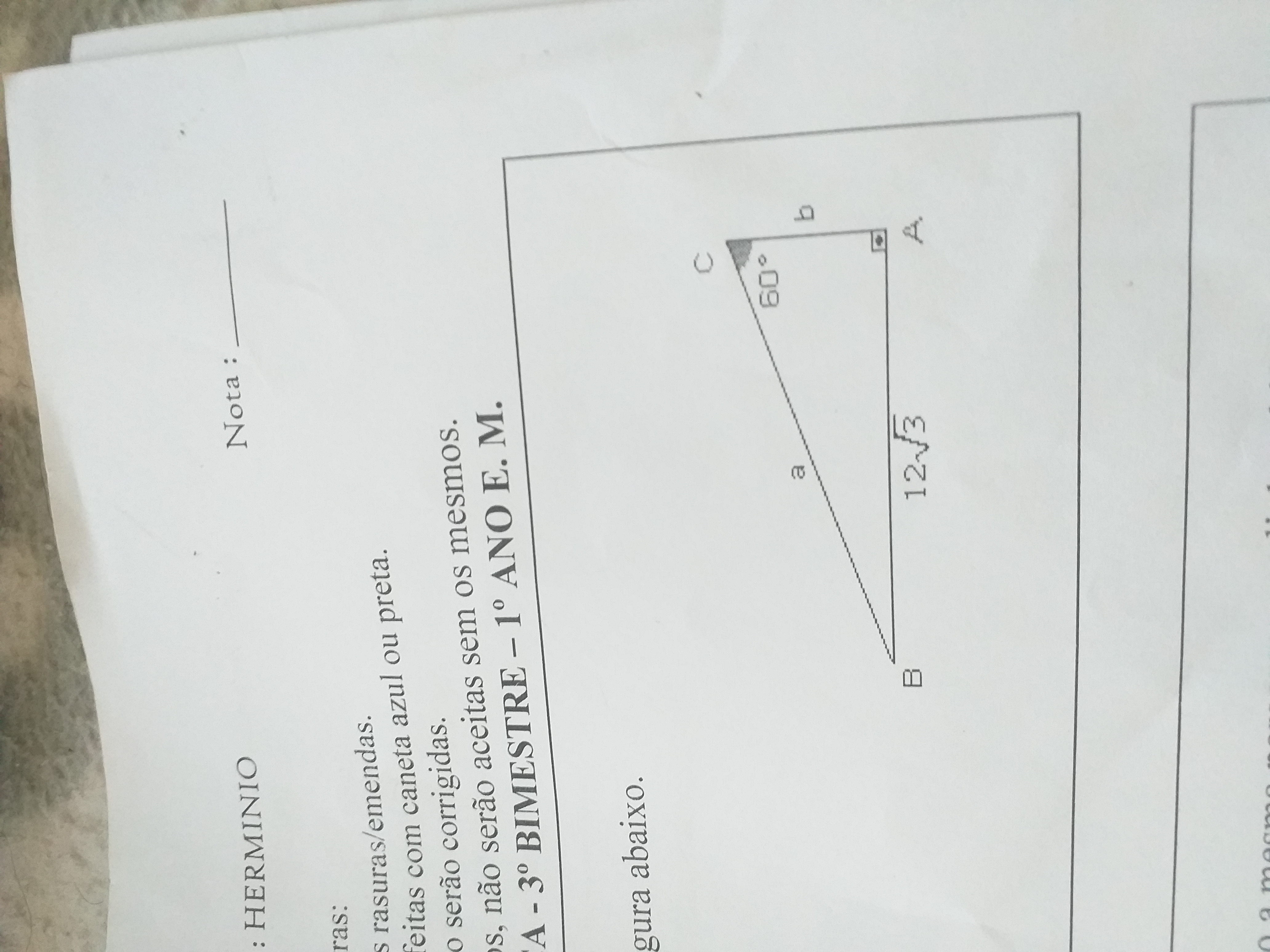
Determine a medida de A e B representadas na figura abaixo?

Fazendo: tg 60º = 12 x raiz de 3 / b     e sendo  tg 60º = raiz de 3 / 2 , o valor de b = 24

Usando o Teorema de Pitágoras:  a² = 24²  +  (12xraiz de 3)² = 31,7

No problema em questão, temos que:

\[\eqalign{\]
\operatorname{sen} 60^\circ = \dfrac{{12\sqrt 3 }}{a} \cr \(\dfrac{{\sqrt 3 }}{2} = \dfrac{{12\sqrt 3 }}{a} \cr \) a = \dfrac{{12\sqrt 3 \cdot 2}}{{\sqrt 3 }} \cr \(\boxed{a = 24} \cr \) \cr \(\tan 60^\circ = \dfrac{{12\sqrt 3 }}{b} \cr \) \sqrt 3 = \dfrac{{12\sqrt 3 }}{b} \cr \(b = \dfrac{{12\sqrt 3 }}{{\sqrt 3 }} \cr \) \boxed{b = 12} \cr} $$