(EURJ 2013) Um cristal com a forma de um prisma hexagonal regular...
após ser cortado e polido, deu origem a um sólido de 12 faces triangulares congruentes. Os vértices desse poliedro são os centros das faces do prisma, conforme representado na figura.
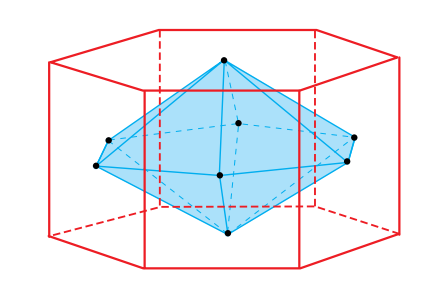
Calcule a razão entre os volumes do sólido e do prisma.
3 resposta(s) - Contém resposta de Especialista
Profª. Thayná Leal (matemática) 
Há mais de um mês
São duas pirâmides hexagonais congruntes.
Altura da pirâmide = h/2 , onde "h" é a altura do prisma.
Note que a medida da aresta da base do prisma (L') = √3/2 L , onde L' é a medida da aresta das pirâmides.
Usando proporção para as áreas, temos:
área da base da pirâmide / área da base do prisma = ( (√3/2) L/L ) ²
= 3/4
Razão entre os volumes:
Volume das pirâmides / Volume do cilindro = 2/3 * 3/4 * 1/2 = 1/4
São duas pirâmides hexagonais congruntes.
Altura da pirâmide = h/2 , onde "h" é a altura do prisma.
Note que a medida da aresta da base do prisma (L') = √3/2 L , onde L' é a medida da aresta das pirâmides.
Usando proporção para as áreas, temos:
área da base da pirâmide / área da base do prisma = ( (√3/2) L/L ) ²
= 3/4
Razão entre os volumes:
Volume das pirâmides / Volume do cilindro = 2/3 * 3/4 * 1/2 = 1/4
Essa pergunta já foi respondida!
Perguntas recomendadas
