(UERJ 2014) Observe o gráfico da função polinomial de R em R definida por...
P(x) = \(2x^3\) - \(6x^2\) + \(3x\) + 2.
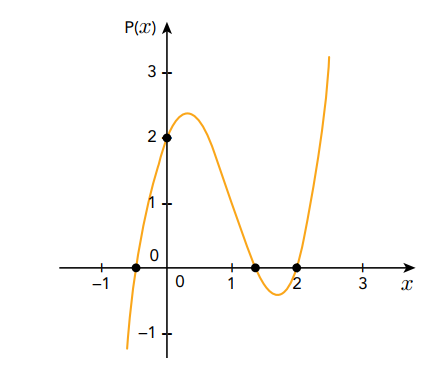
Determine o conjunto solução da inequação P(x) > 0.
💡 3 Respostas
Profª. Thayná Leal (matemática)
Note que x = 2, é uma raíz.
Logo, o polinômio é divísivel por (x-2).
Vamos verificar o quociente:
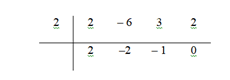
Resulta no polinômio 2x² - 2x - 1
Vamos encontrar as raízes:
2x² - 2x - 1 = 0
a = 2, b = -2 , c = -1
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
\(x = {2 \pm \sqrt{4-4*2*(-1)} \over 4}\)
x' = (2+√ 12)/4 = (1+√ 3)/2
x'' = (1-√ 3)/2
Solução: ] (1-√ 3)/2 , (1+√ 3)/2 [ U ]2 , ∞ [
Thiago Barros
Daniela Gaspar
Solução: ] (1-√ 3)/2 , (1+√ 3)/2 [ U ]2 , ∞ [
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar