(UERJ 2014)
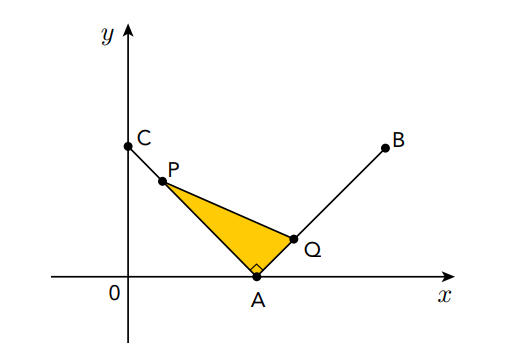
No gráfico acima, estão indicados os pontos A(1,0), B(2,1) e C(0,1), que são fixos, e os pontos P e Q, que se movem simultaneamente. O ponto P se desloca no segmento de reta de C até A, enquanto o ponto Q se desloca no segmento de A até B. Nesses deslocamentos, a cada instante, a abscissa de P é igual à ordenada de Q. Determine a medida da maior área que o triângulo PAQ pode assumir.
💡 2 Respostas
Larinha Silva
4 l uo
Profª. Thayná Leal (matemática)
Vamos encontrar as equações das retas AC e AB do tipo y = ax +b
AC :
(1,0)(0,1)
1 = a*0 +b
b = 1
0 = a + 1
a = -1
equação: -x + 1
AB: (1,0)(2,1)
0 = a +b
1 = 2a + b
0 = -a - b
1 = 2a + b
1 = a
0 = 1 + b
b = - 1
equação: x - 1
Coordenadas de P = (x' , -x' +1)
Coordenadas de Q = (x'+1,x')
Usando distância entre dois pontos, temos:
AP = √[(x'-1)²+(x'+1-0)²] = (1-x')√ 2
AQ = √ [(x'+1-1)²+(x'-0)²] = x' √ 2
Portanto , a área será:
[(1-x')√ 2 *x' √ 2 ]/2 = -x' ² + x'
Como queremos a área máxima, usaremos Yv da parábola:
xV = -b/2a = -1/-2 = 1/2
Yv = - (1/2)² + 1/2 = -1/4 + 1/2 = 1/4
Resposta: 1/4
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Compartilhar