(UERJ 2015) Um cubo de aresta EF medindo 8 dm contém água e está apoiado sobre um plano a de modo que apenas a aresta EF esteja contida nesse plano.
A figura abaixo representa o cubo com a água.
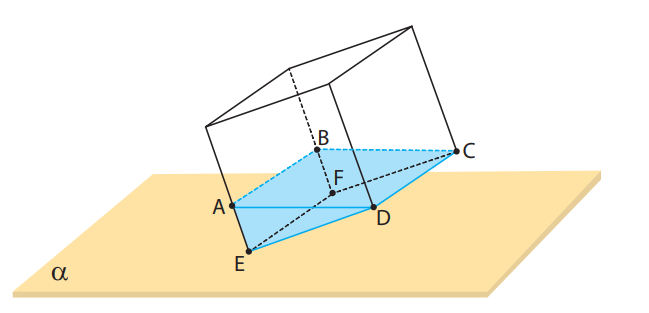
Considere que a superfície livre do líquido no interior do cubo seja um retângulo ABCD com área igual a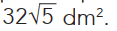 
Determine o volume total, em \(dm^3\), de água contida nesse cubo.
💡 2 Respostas
Jose Augusto
sabemos que:
* a área do retângulo ABCD = 32
* EF = CD = 8 dm
Assim:
32√5 = AD . 8
AD = 4√5 dm
Sobre o triângulo retângulo AED, sabemos que:
AD² = AE² + ED²
(4√5)² = (AE)² + 8²
80 - 64 = AE²
AE = 4 dm
Profª. Thayná Leal (matemática)
Se EF = 8 , temos que AB = 8.
Vamos descobrir a outra medida do lado do retângulo:
8 * aD = 32√ 5
AD = 32√ 5 / 8
AD = 4√ 5 dm
Volume da água =
Precisamos encontrar AE:
(4√ 5)² = 8² + AE²
80 = 64 + AE²
AE = 4
Volume da água (prisma de base triângular) = (8*4)/2 * 8 = 128 dm³
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Compartilhar