(UERJ 2016) Em um triângulo equilátero de perímetro igual a 6 cm, inscreve-se um retângulo
de modo que um de seus lados fique sobre um dos lados do triângulo. Observe a figura:
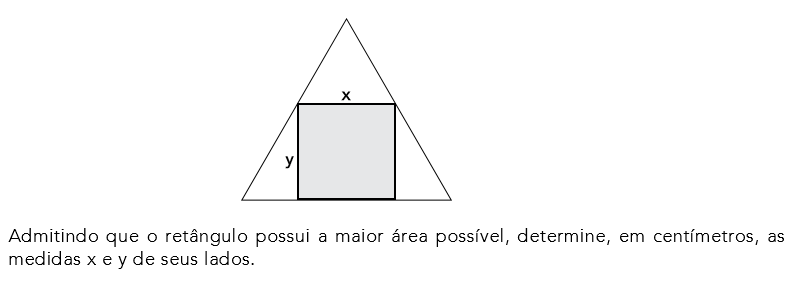
💡 2 Respostas
Felipe Gama
y = √3/2
x = 1
Profª. Thayná Leal (matemática)
perímetro do triângulo = 6
3 L = 6
L = 2 (lado do triângulo)
Altura do triângulo equilátero = L√ 3 /2 = 2√ 3/2 = √ 3.

Usando semelhança entre o triângulo ADB e o triângulo pequeno no lado esquerdo (FEB), temos:
\(y/√ 3 = (1-x/2)/1\)
\(y = √ 3 - (√ 3/2) x \)
Portanto, a área do retângulo será:
\(A = x*y = x(√ 3 - (√ 3/2)x) = (-√ 3/2)x² +√ 3x \)
Trata-se de uma equação do segundo grau e para encontrar a área máxima, precisamos do Xv.
\(Xv = -b/2a = -√ 3/ (2(-√ 3/2)) = -√ 3 /( -√ 3) = 1 \)
Substituindo x , temos que
\(y = √ 3 -√ 3/2 = √ 3/2 cm \)
Resposta: x = 1 cm e y = √ 3/2 cm
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.




Compartilhar