(PUCRJ 2019)Considere um triângulo equilátero ABC de lado 1.
Traçamos um arco de círculo de centro A ligando B a C, como na figura.
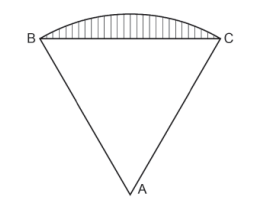
Quanto vale a área da região assinalada, que fica fora do triângulo e dentro do círculo?
💡 2 Respostas
Profª. Thayná Leal (matemática)
Área do setor circular:
(Note que trata-se de um triângulo equilátero, logo, os ângulos são de 60º)
360º ----------------- πr²
60º ----------------- x
360º ------------- π
60º ------------- x
360x = 60π
x = π/6
Área do triângulo: (b*h/2)
altura do triângulo equilátero = l√3/2
Área = (1*√3/2)/2 = √3/4
Portanto, área da região sombreada = π/6 - √3/4 (letra C)
Stefane bonfanti
eu n sei qual a resposta
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Compartilhar