Por favor tenta resolver
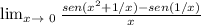
💡 4 Respostas
Letícia Cabral
lim (sin((x^2 + 1)/x) - sin (1/x))/x = lim sin(x + x^-1)/x + lim sin(x^-1)/x
pelo limite fundamente, lim sen(Ku)/u = K, ou seja, é igual à derivada da expressão de x que representa o ângulo do seno, então:
lim sin(x + x^-1)/x = 1 - x^(-2)
lim sin(x^-1)/x = x^(-2)
somando as igualdades -> 1 - x^(-2) + x^(-2) = 1
lim (sin((x^2 + 1)/x) - sin (1/x))/x = 1
Andre Pucciarelli
Para isso, vamos usar uma subsequência:
\(x=2n \pi\)
Substituindo:
\(L=({sen{(2 \pi n)^2+1 \over 2 \pi n}-sen({1 \over 2 \pi }) \over 2 \pi n})\\ L=0\)
Assim, o limite é divergente.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar