qual seria a amplitude do intervalo de classe?

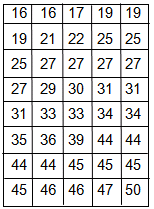
	Os dados a seguir foram coletados numa pesquisa amostral feita em uma instituição. De acordo com os dados, podemos construir uma tabela de dados agrupados. Sendo assim, qual seria a amplitude do intervalo de classe? Regra de Sturges: i = 1 + 3,3 . log n. Considere o log 40 = 1,60.

	a) A amplitude do intervalo de classe é 5,43.
	b) A amplitude do intervalo de classe é 5,41.
	c) A amplitude do intervalo de classe é 6,41.
	d) A amplitude do intervalo de classe é 6,87.

Estatística I

•

UNIASSELVI

6

0

6

0

5

Tais Costa

17/09/2019

💡 5 Respostas

Andre Smaira

12.10.2019

Temos uma amostra de tamanho

\(n=40\)

Pela regra de Sturges, temos que o número de classes da amostra é

i=1+3,3\log n

Considerando

\log 40=1,6

temos

\(i=6,28\)

Como

\(i\)

deve ser inteiro, arredondamos

\(i=6\)

Logo, temos que nossa amostra será divida em 6 intervalos.

A amplitude do intervalo $$a$$ é dado pela diferença entre o limite superior e inferior da amostra sobre o tamanho do intervalo. Temos então: $a=\dfrac{50-16}{6,28}=\dfrac{34}{6,28}=5,41$ Nesse caso, não utilizamos o tamanho do intervalo arredondado para chegar a resposta correta.

Portanto, a alternativa correta é a letra (b).

3

0

Tais Costa

21.09.2019

Muito Obrigada pela resposta!

1

0