Calcule o raio de um átomo de irídio dado que o Ir possui uma estrutura cristalina CFC, uma densidade de 2,4g/cm3, em um peso atômico de 192,2g/mol
💡 2 Respostas
Matheus Tenorio
Sabemos que estrutura de "CFC" possui sua aresta
Pela formula de densidade temos que:
Onde:
"N" = total de atomos em cada célula unitaria
"A" = peso atomico
Na = numero de avogadro
Vc = volume total da célula unitaria
Em um "CFC" temos 8 atomos nos vertices e 6 atomos em cada face:
Na ≈ 6,0*10²³
Levando os dados na formula da densidade ficamos:
64R³/2√2 = 0,05720cm³/10²¹
32R³/√2 = 0,05720cm³/10²¹
32R³ = √2*0,05720cm³/10²¹
R³ = √2*0,05720cm³/(10²¹*32)
R³ ≈ 0,08089cm³/(10²¹*32)
R³ ≈ 0,0025cm³/(10²¹)
R³ ≈ 2,5*10⁻³cm³/(10²¹)
R³ ≈ 2,5cm³/(10³*10²¹)
R³ ≈ 2,5cm³/(10²⁴)
R ≈ ∛2,5cm³/∛(10²⁴)
R ≈ ∛2,5*cm/10⁸
R ≈ 1,35720cm/10⁸
R ≈ 1,35*10⁻⁸cm
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Materiais relacionados
 1 pág.
1 pág. 1 pág.
1 pág.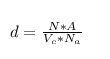
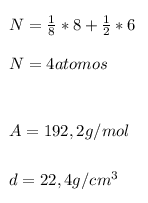
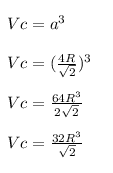






Compartilhar