Atividade 1 - Mecânica dos Sólidos
PERGUNTA 1
-
Ao longo da Unidade 1, verificamos que quando um corpo está se movendo em direção retilínea, ou seja, em uma única direção, o seu movimento é denominado de unidimensional. Caso o corpo esteja se movendo mediante um plano, isto é, em duas direções, o movimento é designado bidimensional (HALLIDAY, 2012). Como exemplo de movimento unidimensional, temos o movimento em linha reta e o movimento quando o ônibus ou o metrô freiam e continuamos a nos mover em linha reta. Já como exemplos de movimento bidimensional, temos o movimento circular e o lançamento de projéteis (movimento no plano xy).
Com base nessas informações e nos assuntos estudados ao longo da Unidade 1, analise o exemplo de um corpo que é lançado do lugar P a uma velocidade de 20 m/s em uma direção e sentido que formam um ângulo de 45 graus com a horizontal, alcançando no ponto Q, de acordo com o que é apresentado na figura a seguir.
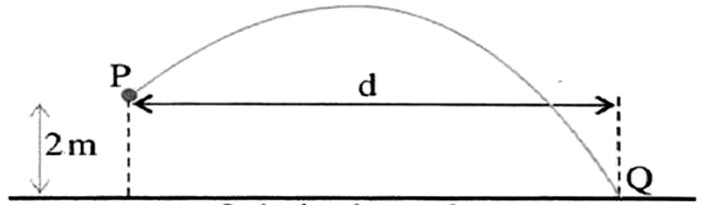
Fonte: Elaborada pelo autor, 2019.
Considerando a resistência do ar como insignificante, avalie o espaço demarcado no esquema, em metros. Adote g = 10 m/s2.
💡 2 Respostas
Reginaldo Medeiros
V0 = 20 m/s
angulo = 450
V0x = 20 cos45 = 10\(\sqrt{2}\)m/s
V0x = 20 sen45 = 10\(\sqrt{2}\)m/s
ponto mais alto
Vy = V0y - gt
0 = 10\(\sqrt{2}\) - 10t
t = \(\sqrt{2}\) s
Vy2 = V0y2 - 2gH
0 = (10\(\sqrt{2}\))2 - 20H
0 = 200 - 20H
H = 10 m
descida
h = 10 + 2 = 12 m
Vy2 = V0y2 + 2gH
Vy2 = 0 + 20*12
VyQ = 4\( \sqrt{15} \)m/s
Vy = V0y + gt
4\( \sqrt{15} \) = 0 + 10t
t = 0,4\( \sqrt{15} \) s
t total = \(\sqrt{2}\)+0,4\( \sqrt{15} \)= 2,9634 s
distancia (horizontal)
S = S0 + V0xt total
d = S- S0 = 10\(\sqrt{2}\) * 2,9634 = 41,9 m
Andre Smaira
A distância percorrida na horizontal, \(d\), será dada por \(d=V_{0x}t\), sendo \(t\) o tempo que o corpo permanece no ar.
Sabemos que o corpo é lançado de uma altura inicial \(h_0=2\;m\). Calculamos primeiro o tempo que ele gastará para chegar ao ponto mais alto da sua trajetória, em que sua velocidade será \(V=0\). Fazemos \(V=V_{0y}-gt_1\), com \(g=10\;m/s^2\). Assim, temos \(t_1=\sqrt2\;s\). Ele gastará então \(t_2=2\sqrt2\;s\) para atingir novamente a altura \(h_0\).
Vamos agora calcular o tempo que ele gastará para atingir o chão, ou seja, \(h=0\). Fazemos \(h=h_0+V_{0y}t+g\dfrac{t^2}2\Rightarrow5t^2+10\sqrt2t-2=0\). Encontrando \(t_3=0,14\;s\).
Assim, o tempo total de movimento é \(t=2,97\;s\) e a distância percorrida será \(\boxed{d=42\;m}\).
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Quem consegue responder essa questão de Mecânica dos Sólidos?
Mecânica dos Sólidos I
•UNINOVE
paulo henrique






Compartilhar