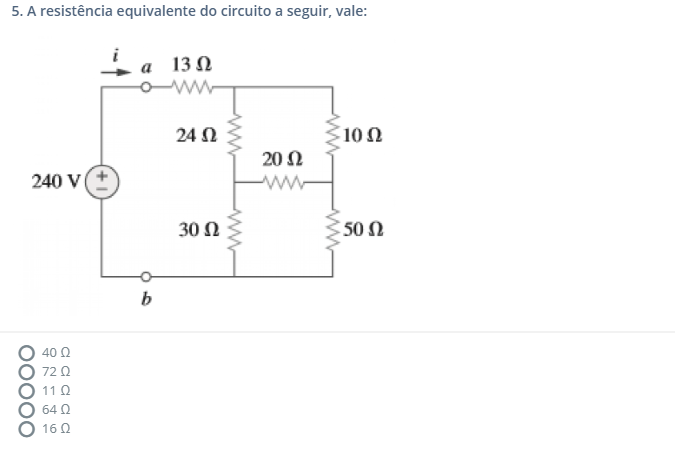
Através do método das malhas, vamos supor correntes circulando nas malhas em sentido horário.

. i1: malha 240V / 13Ω / 24Ω / 30Ω (malha da esquerda)

. i2: malha 10Ω / 20Ω / 24Ω (malha superior direita)

. i3: malha 20Ω / 50Ω / 30Ω (malha inferior direita)

1) Equação da malha i1:

-> 13i1 + 24(i1 - i2) + 30(i1 - i3) = 240

-> 67i1 - 24i2 - 30i3 = 240 (I)

2) Equação da malha i2:

-> 10i2 + 20(i2 - i3) + 24(i2 - i1) = 0

-> - 24i1 + 54i2 - 20i3 = 0 (II)

3) Equação da malha i3:

-> 50i3 + 30(i3 - i1) + 20(i3 - i2) = 0

-> - 30i1 - 20i2 + 100i3 = 0 (III)

Reunindo as equações de (I) a (III):

{ 67i1 - 24i2 - 30i3 = 240

{ - 24i1 + 54i2 - 20i3 = 0

{ - 30i1 - 20i2 + 100i3 = 0

Reescrevendo o sistema de equações na forma matricial A*x = B:

[ 67 -24 -30 ] [ i1 ] [ 240 ]

[ -24 54 -20 ] * [ i2 ] = [ 0 ]

[ -30 -20 100 ] [ i3 ] [ 0 ]

Realizando a operação matricial x = inv(A)*B, os valores das correntes de malha são:

{ i1 = 6 A

{ i2 = 18/5 A

{ i3 = 63/25 A

Como i1 é a corrente que sai da fonte de 240 V, a resistência equivalente Req é:

-> Req = 240/i1

-> Req = 240/6

-> Req = 40Ω

Se gostou, dá um joinha!