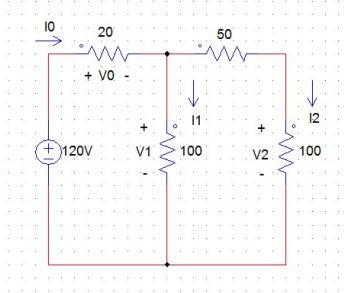
Analise o circuito abaixo e calcule: a) A resistência equivalente b) A corrente I0 c) A tensão V0 d) A corrente I1 e) A corrente I2 f) A tensão V2

a) Resistência equivalente (Req): a resistência vista pelos terminais da fonte de tensão de 120 V é:

-> Req = 20 + 100//(50 + 100)

-> Req = 20 + 100//(150)

-> Req = 20 + 100⋅150/(100 + 150)

-> Req = 20 + 15000/(250)

-> Req = 20 + 60

-> Req = 80 Ω

=======================================

b) Corrente I₀ circulando em sentido horário na malha à esquerda, e corrente I₂ circulando em sentido horário na malha à direita. Portanto, tem-se I₁ = I₀ - I₂.

Equação da malha I₀:

-> 20I₀ + 100(I₀ - I₂) = 120

Dividindo a equação por 20:

-> I₀ + 5(I₀ - I₂) = 6

-> I₀ + 5I₀ - 5I₂ = 6

-> 6I₀ - 5I₂ = 6 (I)

Equação da malha I₂:

-> 50I₂ + 100I₂ + 100(I₂ - I₀) = 0

Dividindo a equação por 50:

-> I₂ + 2I₂ + 2(I₂ - I₀) = 0

-> I₂ + 2I₂ + 2I₂ - 2I₀ = 0

-> 5I₂ = 2I₀

-> I₂ = 0,4I₀ (II)

Substituindo a equação (II) em (I), o valor de I₀ é:

-> 6I₀ - 5I₂ = 6 (I)

-> 6I₀ - 5⋅0,4I₀ = 6

-> 6I₀ - 2I₀ = 6

-> 4I₀ = 6

-> I₀ = 1,5 A

=======================================

c) Com I₀ = 1,5 A, a tensão V₀ no resistor de 20 Ω é:

-> V₀ = 20I₀

-> V₀ = 20⋅1,5

-> V₀ = 30 V

=======================================

e) Substituindo I₀ = 1,5 A na equação (II), o valor de I₂ é:

-> I₂ = 0,4I₀ (II)

-> I₂ = 0,4⋅1,5

-> I₂ = 0,6 A

=======================================

d) Com I₀ = 1,5 A e I₂ = 0,6 A, o valor da corrente I₁ é:

-> I₁ = I₀ - I₂

-> I₁ = 1,5 - 0,6

-> I₁ = 0,9 A

=======================================

f) Com I₂ = 0,6 A, a tensão V₂ no resistor de 100 Ω é:

-> V₂ = 100I₂

-> V₂ = 100⋅0,6

-> V₂ = 60 V

=======================================

Se gostou, dá um joinha!