Calcule o valor da corrente Ic do circuito seguinte:
💡 1 Resposta
Ricardo Proba
Por análise nodal, tem-se o nó V₁ acima do resistor de 40 Ω e o nó V₂ acima do resistor de 15 Ω.
------------------------------------------------------------
1) Equação nodal de V₁:
-> (V₁ - 120)/10 + V₁/40 + (V₁ - V₂)/30 = 0
Multiplicando a equação por 120:
-> 12(V₁ - 120) + 3V₁ + 4(V₁ - V₂) = 0
-> 12V₁ - 1440 + 3V₁ + 4V₁ - 4V₂ = 0
-> 19V₁ - 4V₂ = 1440 (I)
2) Equação nodal de V₂:
-> (V₂ - V₁)/30 + V₂/15 + V₂/30 = 0
Multiplicando a equação por 30:
-> (V₂ - V₁) + 2V₂ + V₂ = 0
-> 4V₂ - V₁ = 0
-> V₁ = 4V₂ (II)
------------------------------------------------------------
Substituindo a equação (II) em (I), o valor de V₂ é:
-> 19V₁ - 4V₂ = 1440 (I)
-> 19⋅(4V₂) - 4V₂ = 1440
-> 76V₂ - 4V₂ = 1440
-> 72V₂ = 1440
-> V₂ = 1440/72
-> V₂ = 20 V
------------------------------------------------------------
Portanto, a corrente Ic no resistor de 30 Ω é:
-> Ic = V₂/30
-> Ic = 20/30
-> Ic = 0,67 A
------------------------------------------------------------
Solução: Ic = 0,67 A.
Se gostou, dá um joinha!
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta.
Perguntas relacionadas
Materiais relacionados
 1 pág.
1 pág. 1 pág.
1 pág.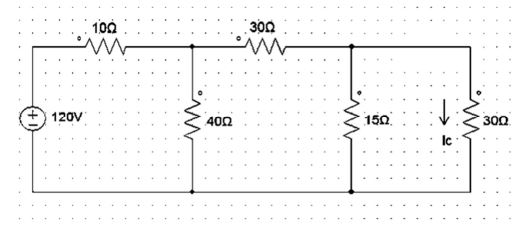






Compartilhar