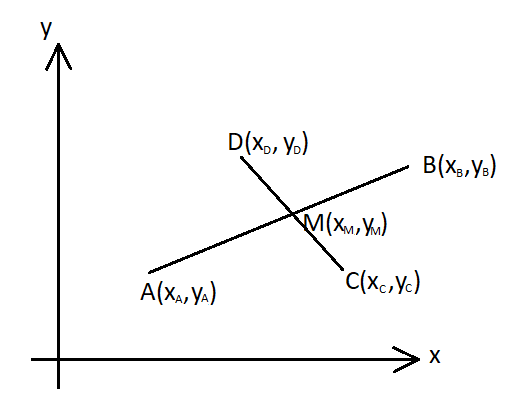
Dois segmentos AB e CD se interceptam em um ponto M, o qual é ponto médio dos dois segmentos. Mostre que AC = BD?

Ponto médio M:

{ xM = (xA + xB)/2 = (xC + xD)/2 (I)

{ yM = (yA + yB)/2 = (yC + yD)/2 (II)

-----------------------------------------------------------------

A partir da equação (I), tem-se o seguinte:

-> (xA + xB)/2 = (xC + xD)/2

-> xA + xB = xC + xD

-> xA - xC = xD - xB

-> xA - xC = xD - xB

-> (xA - xC)² = (xD - xB)²

-> (xA - xC)² = (xB - xD)² (III)

Analogamente, a partir da equação (II):

-> (yA - yC)² = (yB - yD)² (IV)

-----------------------------------------------------------------

A equação da distância entre os pontos A(xA, yA) e C(xC, yC) é:

-> AC = √[ (xA - xC)² + (yA - yC)² ]

Substituindo as equações (III) e (IV):

-> AC = √[ (xA - xC)² + (yA - yC)² ]

-> AC = √[ (xB - xD)² + (yB - yD)² ]

-> AC = BD

-----------------------------------------------------------------

Portanto, foi comprovada a igualdade AC = BD.

Se gostou, dá um joinha!