Determinar a vazão de contribuição em l/s*ha em uma cidade onde a distribuição da população é de 110 hab/ha, adotando os valores da Norma de Entidades
|
Determinar a vazão de Contribuição em l / s * ha em Uma Cidade Onde a Distribuição da População E de 110 hab / ha, adotando OS Valores da Norma de Entidades Públicas Federais. Sabe-se that, em meios de comunicação, na área a esgotar existem 170m de Ruas POR hectare.
Dados: - Quota "per capta" 200 l / hab * dia. - Coeficiente do Dia de Maior Distribuição: k 1 = 1,2. - Coeficiente da hora de Maior Distribuição: K2 = 1,5. - Relação esgoto Água admitida 0,85. - Vazão de infiltração Nos coletores 0,0005 l / s * m.
|
||
|
Q = 0,57 l / s * ha |
||
|
Q = 0,57 l / s * ha |
||
|
Q = 0,47 l / s * ha |
||
|
Q = 0,97 l / s * ha |
||
|
Q = 0,87 l / s * ha |
||
💡 2 Respostas
Luiz -
Olá. Sou o Luiz, estou graduando em eng civil e resolvo questões de diversas matérias da área de exatas. Muitos da Uniube já utilizaram dos meus serviços e continuo procurando por alunos. Se interessar, entre em contato pelo whatsapp: 31 98464-2756. Abç
RD Resoluções
Na resolução deste problema, devemos colocar em prática nosso conhecimento sobre Saneamento.
Para calcular a vazão, devemos aplicar a fórmula fornecida pelo exercício, isto é:
\(Q=\dfrac{k_1\cdot k_2\cdot P\cdot q\cdot C}{86.400}\)
No problema em questão, tem-se que \(k_1=1,2\), \(k_2=1,5\), \(P=110\text{ habitantes}\), \(q=200\text{ }\frac{\text L}{\text{hab}\cdot\text{dia}}\) e \(C=0,85\). Substituindo tais dados, resulta que:
\(\begin{align} Q&=\dfrac{1,2\cdot 1,5\cdot 110\cdot 200\cdot 0,85}{86.400} \\&=0,39\text{ }\frac{\text L}{\text s\cdot \text{ ha}} \end{align}\)
Além disso, devemos a vazão de infiltração nos coletores:
\(\begin{align} Q'&=0,0005\text{ }\frac{\text L}{\text s\cdot \text m}\cdot 170 \\&=0,085\text{ }\frac{\text L}{\text s\cdot \text{ ha}} \end{align}\)
Somando as vazões, vem que:
\(0,39\text{ }\frac{\text L}{\text s\cdot \text{ ha}}+0,085\text{ }\frac{\text L}{\text s\cdot \text{ ha}}\approx 0,47\text{ }\frac{\text L}{\text s\cdot \text{ ha}}\)
Portanto, a vazão de contribuição é de, aproximadamente, \(\boxed{ 0,47\text{ }\frac{\text L}{\text s\cdot \text{ ha}}}\).
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
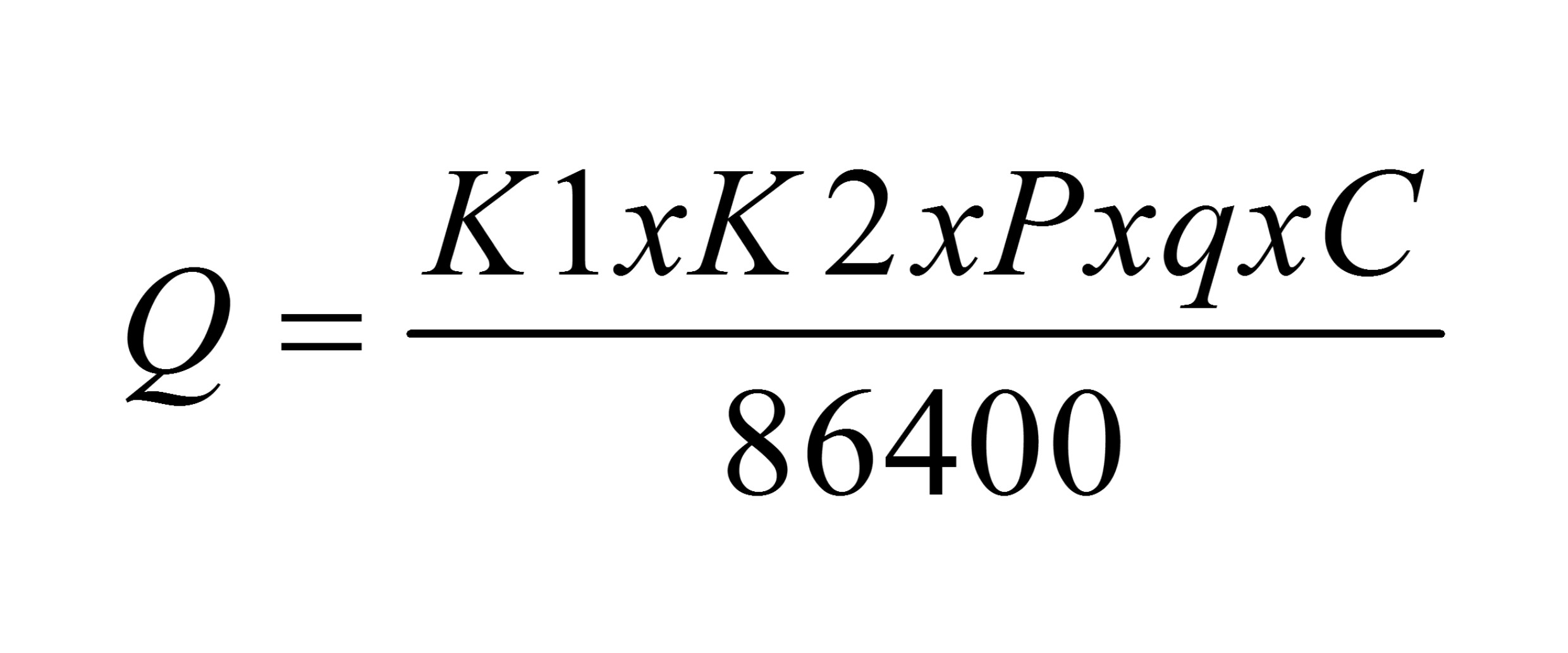






Compartilhar