quando eque uma função è injectiva
💡 1 Resposta
Clecirlei Neris da Silva
Denominamos função injetora, a função que transforma diferentes elementos do domínio (conjunto A) em diferentes conjuntos da imagem (elementos do conjunto B), ou seja, não existe elemento da imagem que possui correspondência com mais de um elemento do domínio. Em uma linguagem matemática formal teríamos:
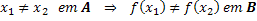
RD Resoluções
Uma função é injetiva quando, para um determinado x1 e um x2, temos \(\boxed{f(x1) \neq f(x2)}\)
Por exemplo, a função \(x²-4\) não é injetiva pois para \(x1=2\) e \(x2=-2\), por exemplo, temos:
\(f(2)= 2²-4 =0\)
\(f(-2) = (-2)²-4 =0\)
Ou seja, para valores diferentes \(( 2\: \: -2)\) a função deu o mesmo resultado (0)
Já a função \( x-1\) é injetiva, pois para \(x1=1\) e \(x1=0\), por exemplo, o resultado é diferente:
\(f(1)=1-1=0\\ f(0)=0-1= -1\)
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar