Como calcular parcelamentos com juros compostos?
💡 4 Respostas
Andre Smaira
Neste exercício, serão aplicados os conhecimentos sobre matemática financeira. Para isso, será utilizado um exemplo numérico.
Uma pessoa realizou uma compra de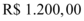 
, pagou uma entrada de 
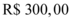e pagará o restante em cinco prestações mensais e iguais a uma taxa de juros composta mensal de 
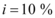. Determine o valor de cada parcela.
No mês 
(presente), foi paga a entrada de 
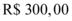. Portanto, o valor que resta pagar é:
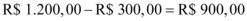
O valor de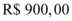 
será dividido em cinco parcelas iguais. Portanto, tem-se o valor presente 
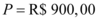, o valor de cada prestação 
, juros compostos mensais de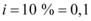 
e 
meses.
Para achar o valor de 
, será utilizada a seguinte fórmula para juros compostos:
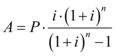
Substituindo os valores conhecidos, o valor de 
é:
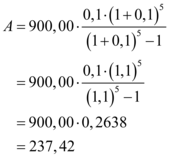
Concluindo, considerando juros compostos, o valor de cada prestação é, aproximadamente:
Andre Smaira
Neste exercício, serão aplicados os conhecimentos sobre matemática financeira. Para isso, será utilizado um exemplo numérico.
Uma pessoa realizou uma compra de 
, pagou uma entrada de 
e pagará o restante em cinco prestações mensais e iguais a uma taxa de juros composta mensal de 
. Determine o valor de cada parcela.
No mês 
(presente), foi paga a entrada de 
. Portanto, o valor que resta pagar é:
O valor de 
será dividido em cinco parcelas iguais. Portanto, tem-se o valor presente 
, o valor de cada prestação 
, juros compostos mensais de 
e 
meses.
Para achar o valor de 
, será utilizada a seguinte fórmula para juros compostos:
Substituindo os valores conhecidos, o valor de 
é:
Concluindo, considerando juros compostos, o valor de cada prestação é, aproximadamente:
RD Resoluções
Neste exercício, serão aplicados os conhecimentos sobre matemática financeira. Para isso, será utilizado um exemplo numérico.
Uma pessoa realizou uma compra de 
, pagou uma entrada de 
e pagará o restante em cinco prestações mensais e iguais a uma taxa de juros composta mensal de 
. Determine o valor de cada parcela.
No mês 
(presente), foi paga a entrada de 
. Portanto, o valor que resta pagar é:
O valor de 
será dividido em cinco parcelas iguais. Portanto, tem-se o valor presente 
, o valor de cada prestação 
, juros compostos mensais de 
e 
meses.
Para achar o valor de 
, será utilizada a seguinte fórmula para juros compostos:
Substituindo os valores conhecidos, o valor de 
é:
Concluindo, considerando juros compostos, o valor de cada prestação é, aproximadamente:
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Como calcular juros compostos com pagamento da 1ª parcela apos o 3º mês
Matemática Financeira
•UNOPAR
Felipe Martins
Compartilhar