como calcular EDO

olução particular - Obtida da geral, mediante condições dadas (chamadas condições iniciais ou condições de contorno).

Conclusão:

Portanto, a solução de uma equação diferencial ordinária (EDO) é uma função que não contém derivadas nem diferenciais e que satisfaz a equação dada (ou seja, a função que, substituída na equação dada, a transforma em uma identidade).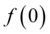

Contextualização:

Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.

Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).

Classificação

Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.

Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.

Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.

Exemplos:

, tem ordem 1 e grau 1

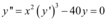
, tem ordem 2 e grau 3

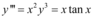
, tem ordem 3 e grau 3

Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 04/10/2018

Resolução:

A solução de uma equação diferencial é uma função que não contém derivadas nem diferenciais e que satisfaz a equação dada (ou seja, a função que, substituída na equação dada, a transforma em uma identidade).

Ex: Equação diferencial ordinária:

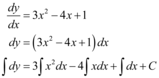
Portanto, a solução geral seria:

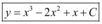
Uma solução particular pode ser obtida da geral através, por exemplo, da condição   (condição inicial)

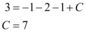
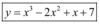
Observação: Em qualquer dos dois casos, a prova pode ser feita derivando a solução e, com isso, voltando à equação dada.

As soluções se classificam em:

Solução geral - apresenta n constantes independentes entre si (n = ordem da EDO). Essas constantes, de acordo com a conveniência, podem ser escritas 

Contextualização:

Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.

Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).

Classificação

Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.

Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.

Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.

Exemplos:

, tem ordem 1 e grau 1

, tem ordem 2 e grau 3

, tem ordem 3 e grau 3

Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 04/10/2018

Resolução:

A solução de uma equação diferencial é uma função que não contém derivadas nem diferenciais e que satisfaz a equação dada (ou seja, a função que, substituída na equação dada, a transforma em uma identidade).

Ex: Equação diferencial ordinária:

Portanto, a solução geral seria:

Uma solução particular pode ser obtida da geral através, por exemplo, da condição (condição inicial)

Observação: Em qualquer dos dois casos, a prova pode ser feita derivando a solução e, com isso, voltando à equação dada.

As soluções se classificam em:

Solução geral - apresenta n constantes independentes entre si (n = ordem da EDO). Essas constantes, de acordo com a conveniência, podem ser escritas

Solução particular - Obtida da geral, mediante condições dadas (chamadas condições iniciais ou condições de contorno).

Conclusão:

Portanto, a solução de uma equação diferencial ordinária (EDO) é uma função que não contém derivadas nem diferenciais e que satisfaz a equação dada (ou seja, a função que, substituída na equação dada, a transforma em uma identidade).