(PUCRJ 2013)O triângulo ABC da figura abaixo tem área 25 e vértices A = (4,5), B = (4,0) e C = (c,0).
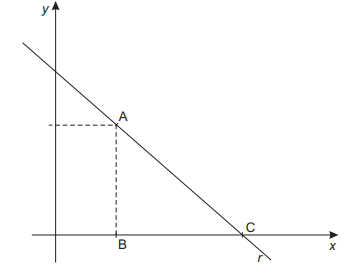
A equação da reta r que passa pelos vértices A e C é:
💡 2 Respostas
Rubeka Sadeq
ejam os vértices do triângulo os pontos A(4,5), B(4,0) e C(x,0).
A área do triângulo é dada por:
A base b é o segmento BC e a altura h o segmento AB.
Vamos calcular o comprimento destes segmentos:
Agora substituindo os valores encontrados na fórmula da área do triângulo:
Portanto, já temos o ponto C(14,0) e podemos achar a equação da reta que passa pelos pontos A e C.
Como se trata de uma reta, temos uma equação do primeiro grau, que é definida por:
y = ax + b
O coeficiente a (coeficiente angular - que na verdade é o valor da tangente do ângulo da reta) pode ser encontrado fazendo:
Já temos o coeficiente angular da equação, basta substituí-lo na fórmula que acabamos de ver:
A alternativa correta é a letra d.
Outra forma simples de encontrar a equação é montando um sistema:
Seja a equação do primeiro grau y = ax + b (mesmo que ax + b = y), temos:
Para o ponto A(4,5) ⇒ a·4 + b = 5
Para o ponto C(14,0) ⇒ a·14 + b = 0
Assim, montamos o sistema:
a·4 + b = 5
a·14 + b = 0
Multiplicando a primeira linha por -1, o sistema fica assim:
-4a - b = - 5
14a + b = 0
Somando as linhas, temos:
10a + 0 = -5 ⇒ 10a = -5 ⇒ a = -5/10 ⇒ a = -1/2
Agora que temos o valor do coeficiente a, substituímos numa das equações do sistema para acharmos o valor de b:
a·4 + b = 5 ⇒ (-1/2)·4 + b = 5 ⇒ -2 + b = 5 ⇒ b = 7
Agora substituímos os valores dos coeficiente encontrados e obtemos a equação procurada:
y = ax + b ⇒ y = (-1/2)x + 7 ⇒ y = -x/2 + 7
Outra forma também fácil de achar a equação da reta é através do determinante da matriz. Dê uma pesquisada na internet.
Leia mais em Brainly.com.br - https://brainly.com.br/tarefa/7418477#readmore
Profª. Thayná Leal (matemática)
Temos que área do triângulo = |D|/2
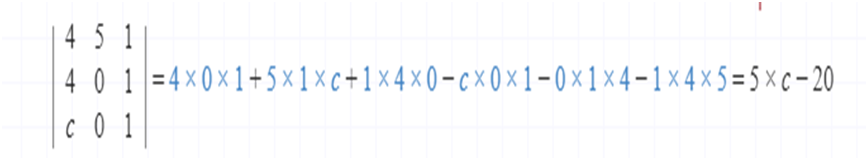
(5c - 20)/2 = 25
5c - 20 = 50
5c = 70
c = 14
Vamos montar a equação da reta que passa por A(4,5) e C(14,0)
y = ax + b
5 = 4a +b
0 = 14a +b
Resolvendo o sistema:
-5 = -4a -b
0 = 14a +b
-5 = 10a
a = -5/10
a = -1/2
0 = 14a +b
0 = 14(-1/2) +b
0 = -7 +b
b = 7
Função: -1/2 x + 7
y = -x/2 + 7 (letra D)
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar