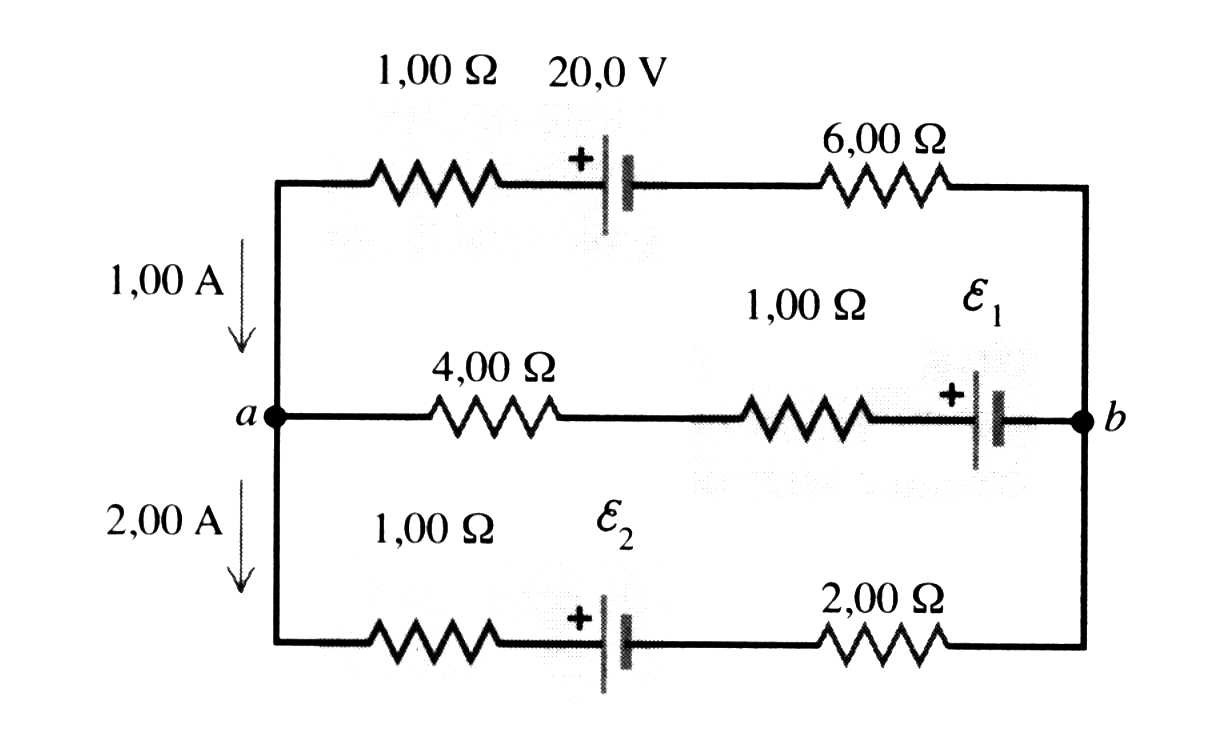
Observe o circuito da figura abaixo e determine a) As forças eletromotrizes E1 e E2 b) O valor da corrente elétrica que atravessa o resistor 4

Aplicando o método da análise nodal no nó A, a corrente i que entra no nó A através do resistor de 4,00 Ω é:

-> i + i1 = i2

-> i + 1 = 2

-> i = 1 A

A corrente i parte do nó b, passa pela bateria E1, passa pelo resistor de 1,00 Ω, passa pelo resistor de 4,00 Ω e chega no nó a. Portanto, com base no circuito, as três possíveis equações de Vab são:

{ Vab = - 6i1 + 20 - 1i1 -> { Vab = 20 - 7i1 (I)

{ Vab = - 4i - 1i + E1 -> { Vab = E1 - 5i (II)

{ Vab = 1i2 + E2 + 2i2 -> { Vab = E2 + 3i2 (III)

Pela equação (I), o valor de Vab é:

-> Vab = 20 - 7i1

-> Vab = 20 - 7*1

-> Vab = 13 V

Portanto, pela equação (II), o valor de E1 é:

-> Vab = E1 - 5i

-> E1 = Vab + 5i

-> E1 = 13 + 5*1

-> E1 = 18 V

E pela equação (III), o valor de E2 é:

-> Vab = E2 + 3i2

-> E2 = Vab - 3i2

-> E2 = 13 - 3*2

-> E2 = 13 - 6

-> E2 = 7 V

Se gostou, dá um joinha!