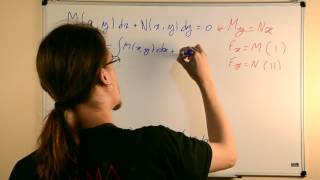
Agora, formalizaremos o método de resolução para equações exatas demonstrando fatos necessários e fazendo algumas observações fundamentais. No fim, resolveremos o exemplo visto na primeira parte da aula. Para ver uma parte específica do vídeo, clique em um dos indicadores abaixo! 0:00 Formalização: hipóteses 1:18 Descrição do método 2:00 Utilizando a primeira condição de exatidão: integral parcial 3:05 Observação fundamental sobre integrais parciais e obtenção da função potencial 4:16 Utilizando a segunda condição de exatidão: derivada parcial 5:27 Observação fundamental sobre a obtenção da função "constante" da integração parcial 6:05 Demonstração que a função "constante" pode ser obtida usando o fato de a equação ser exata 9:04 Obtenção da função potencial 10:22 Solução da equação diferencial 10:52 Observação sobre modos análogos de resolução começando pela outra variável 11:51 Resolução do exemplo visto na primeira parte da aula obtendo a função potencial 13:04 Verificando se a equação é exata 14:17 Usando a primeira condição: integral parcial 14:55 Usando a segunda condição: derivada parcial 15:28 Obtenção da função "constante" 16:07 Determinação da função potencial 16:38 Solução da equação diferencial do exemplo Esse curso e muitos outros estão disponíveis no clubeMAKER - www.clubemaker.com.br/cursos Se houver dúvidas, postem nos comentários ou no fórum do clubeMAKER. Tentaremos esclarecer o máximo de dúvidas que pudermos! Bons estudos! Produção: Lucas Etcheverria e Vinícius Fratin