As afirmativas a seguir se referem ao efeito da flutuação amostral nos testes de hipóteses

acredito que as duas são verdadeiras.

Pode-se distinguir dois grandes tipos de flutuações. A flutuação regular, igualmente conhecida como flutuação cíclica, tem lugar quando existem períodos estacionários (etapas de crescimento sucedem-se a épocas de contracção). A flutuação irregular, em contrapartida, é determinada por modificações que não são periódicas e que obedecem a alterações que não são habituais.

Uma amostra estatística consiste em um subconjunto representativo, ou seja, em um conjunto de indivíduos retirados de uma população, a fim de que seu estudo estatístico possa fornecer informações importantes sobre aquela população.

Suponha agora que queremos testar hipóteses do tipo

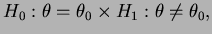
ou seja 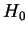 é uma hipótese simples e  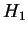é uma alternativa bilateral. Como veremos nas próximas seções este tipo de teste pode ser útil na comparação de tratamentos. O problema é que neste caso não existe um teste UMP para estas hipóteses, i.e. não é possível construir um teste cuja probabilidade de rejeitar  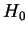seja maximizada quando ela é falsa.

Alternativamente poderiamos construir testes tais que as chances de rejeitar 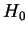 sejam maiores quando ela é falsa do que quando ela é verdadeira. Isto nos leva à definição de testes não viesados a seguir.

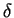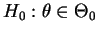
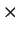
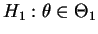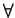
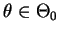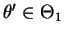Um teste  é dito ser não viesado para as hipóteses    se   e  então 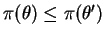. Caso contrário o teste é dito viesado. 
 

Ou seja, em testes não viesados a probabilidade de rejeitar 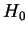 quando ela é falsa é no mínimo tão grande quanto para  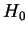verdadeira.

Podemos agora tentar construir testes para hipóteses bilaterais que sejam UMP dentro da classe de testes não viesados. Se a distribuição pertence à família exponencial, pode-se mostrar que se 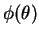 for uma função estritamente crescente em 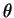então o teste UMP não viesado de nível  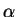para 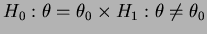 aceita  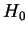quando 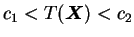. As constantes  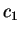e 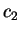 são obtidas de modo que .

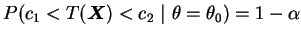Portanto, somente assertiva II é verdadeira.